Bar Bending Schedule Formulas As Per IS:2502-1963

What Is Bar Bending Schedule?

Bar bending is calculating steel quantity that calls bar bending schedule. The preparation of bar bending schedules is one of the final stages in any concrete design following the preparation and detailing of the working drawings.

Whereas the procedure is generally straightforward, it does require a certain amount of calculation which can readily be carried out with the aid of a computer program.

The program in this section calculates the lengths of reinforcing bars required and outputs a bar bending schedule table together with the total weight of steel.

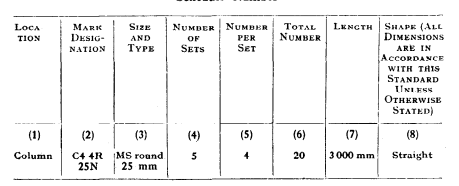
Format of Bar Bending Schedule as per Code IS:2502-196

Location	Mark Designation	Size and Type	Number Per Set	Number of Sets	Total Number	Length	Shape ( All Dimensions Are in Accordance with This Standard Unless Otherwise Stated)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Column	C4 4R 25 N	MS Road 25 mm	5	4	20	3000	Straight

Also, read: What Is Construction Contract | Types of Engineering Contracts | Percentage-Rate Contract

Bar Bending Schedule Use Formulas

1. Unit Weight of Steel Bars

Density = Mass (weight of steel) / Volume

Density = 7850 Kg / m³ Steel Bar
Mass = Weight of Steel
D = Dia of Bar in mm
L = Lenght of M
Volume = πD² /4 x 1000 mm
Weight of Steel = (7850) x (πD² x L/4 )
Weight of Steel = (7850/1000 x 1000 x 1000 ) x ( 3.14 D² /4 )
Weight of Steel = (7850/1000 x 1000 x ~~1000~~ ) x ( 3.14 D² x ~~1000~~ x/4 )
Weight of Steel = 0.00785 x 0.785 D²
Weight of Steel =0.00616225 x D²
Weight of Steel = (0.00616225/1) x (D²/1 )
Weight of Steel = D² / 162.27 kg/m

Example of 12 mm dia bar steel weight

Op-1 of calculation steel weight

Weight of Steel = D² / 162.27 mm
Weight of Steel = 12² / 162.27 mm
Weight of Steel = 144 / 162.27 mm
Weight of Steel = 0. 8874 Kg/m

Op-2 of calculation steel weight

Weight of Steel = (7850) x (π12² x L/4 )
Weight of Steel = (7850/1000 x 1000 x 1000 ) x ( 3.14 12² /4 )
Weight of Steel = (7850/1000 x 1000 x ~~1000~~ ) x ( 3.14 12² x ~~1000~~ x/4 )
Weight of Steel = 0.00785 x 0.785 12²
Weight of Steel =0.00616225 x 144
Weight of Steel = (0.00616225 x 144)
Weight of Steel = 0.8874 Kg/m

Also, read: Curing In Construction | Concrete Cure Time | Methods of curing

2. Plan Bar Length

L = Lenght of Steel

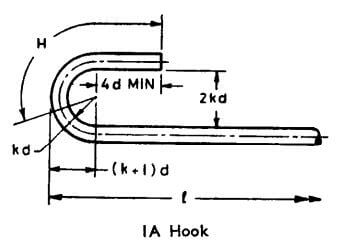
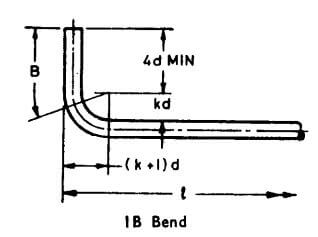
3. Bends and Hooks Forming End Anchorages ( As per IS 2502:1963 )

Here

k in 2 in the case of Mild Steel conforming, ( As per IS 2502:1963, P-6, Note-1 )
k in 3 in the case of Medium Tensile Steel conforming, ( As per IS 2502:1963, P-6, Note-1 )
k in 4 in the case of Cold-worked Steel conforming, ( As per IS 2502:1963, P-6, Note-1 )

Most IMP (As per IS 2502:1963, P-6, Table-II, Note )

H = Hook allowance taken as 9d, 11d, 13d, and 17d for k values 2, 3, 4 and 6 respectively and rounded off to the nearest 5 mm, but not less than 75 mm.
B = Bend allowance is taken as 5d, 5.5d, 6d, and 7d for k values 2, 3, 4 and 6 respectively and rounded off to the nearest 5 mm, but not less than 75 mm.

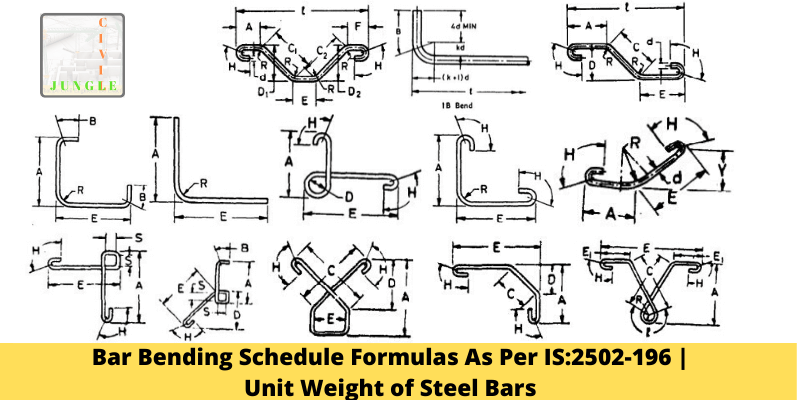
4. Bar Bending Schedule Formulas as below (As per IS 2502:1963, P-8, Table-III )

Measurement of Bending Dimensions of Bars for Reinforced Concrete ( As per IS 2502:1963, P-8, Table-III )

Also, read: What Is Sieve Analysis Test | Sive Analysis Test for Coarse Aggregate | Sive Analysis Test for Fine Aggregate

Ref No.	Method of Measurement of Bending Dimensions	Approx Total Length of Bar (L) Measured Along Centre Line	Sketch and Dimensions to Be Given in Schedule	Approx Total Length of Bar (L) Measured Along Centre Line – Mild Steel	Approx Total Length of Bar (L) Measured Along Centre Line – Medium Tensile Steel	Approx Total Length of Bar (L) Measured Along Centre Line – Cold-worked Steel
A		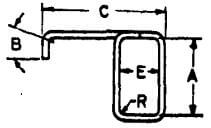2A + E + C +9d + B		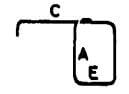2A + E + C +9d + 6d 2A + E + C +15d	2A + E + C +9d + 7d 2A + E + C +16d	2A + E + C +9d + 8d 2A + E + C +17d
B		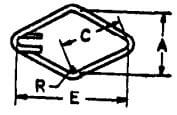4C + 24d		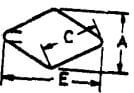4C + 24d	4C + 24d	4C + 24d
C		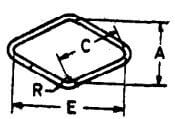4C + 20d		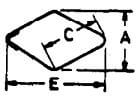4C + 20d	4C + 20d	4C + 20d
D		2A + 3D + 22d		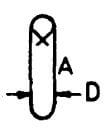2A + 3D + 22d	2A + 3D + 22d	2A + 3D + 22d
E		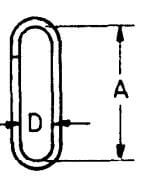2A + 3D + 22d		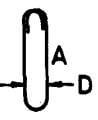2A + 3D + 22d	2A + 3D + 22d	2A + 3D + 22d
F		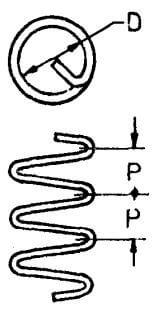Where P is not greater than D/5 N = Number of complete and fractional turns D = Internal dia P = Pitch of helix d = Size of barN π (D + d) + 8d	–	N π (D + d) + 8d	N π (D + d) + 8d	N π (D + d) + 8d
G		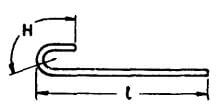L + H		L+H = L + 4d+ d+2kd = L + 4d +4d +d = L + 9d	L+H = L + 4d+ d+2kd = L + (2 x 3)d +4d +d = L + 11d	L+H = L + 4d+ d+2kd = L + (2 x 4 )d +4d +d = L + 13d
H		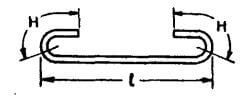L + 2H		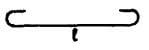L+2H = L + 2 x (4d+ d+2kd) = L + ( 4d +4d +d) x2 = L + 18d	L+2H = L + 2 x (4d+ d+2kd) = L + ((2 x 3)d +4d +d ) x 2 = L + 22d	L+2H = L + 2 x (4d+ d+2kd) = L + ((2 x 4 )d +4d +d ) x 2 = L + 26d
I		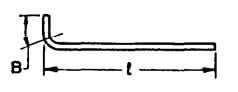L + B		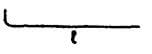L + B = L +4d + kd = L +4d + 2d = L +6d	L + B = L +4d + kd = L +4d + 3d = L +7d	L + B = L +4d + kd = L +4d + 4d = L +8d
J		L + 2B		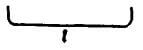L + 2B = L + 2x (4d + kd) = L +2 x (4d + 2d) = L +12d	L + 2B = L + 2x (4d + kd) = L +2 x (4d + 3d) = L +14d	L + 2B = L + 2x (4d + kd) = L +2 x (4d + 4d) = L +16d
K		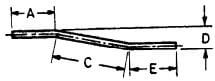Where C is more than 3DA + C + E		A + C + E	A + C + E	A + C + E
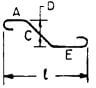
L		If angle with horizontal is 45^o or less, and R is 12d or less A + C + E + 2H or L + 2H + C – √ ( C² – D² )		A + C + E + 18d or L + 18d + C – √ ( C² – D² )	A + C + E + 22d or L + 22d + C – √ ( C² – D² )	A + C + E + 26d or L + 26d + C – √ ( C² – D² )
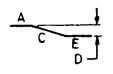
M		If angle with horizontal is 45^o or less, and R is 12d or less A + C1 + C2 + E + F +2H or L +C1 + C2 + 2H – √ ( C1² – D1² ) – √ ( C2² – D2² )		A + C1 + C2 + E + F +18d or L +C1 + C2 + 18d – √ ( C1² – D1² ) – √ ( C2² – D2² )	A + C1 + C2 + E + F +22d or L +C1 + C2 + 22d – √ ( C1² – D1² ) – √ ( C2² – D2² )	A + C1 + C2 + E + F +26d or L +C1 + C2 + 26d – √ ( C1² – D1² ) – √ ( C2² – D2² )
N		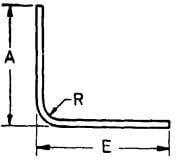A + E – 0.5 R – d		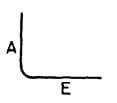A + E – 0.5 R – d	A + E – 0.5 R – d	A + E – 0.5 R – d
O		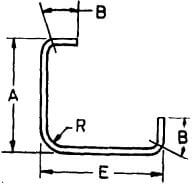A + E – 0.5 R – d + 2B		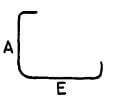A + E – 0.5 R – d + 12d	A + E – 0.5 R – d + 14d	A + E – 0.5 R – d + 16d
P		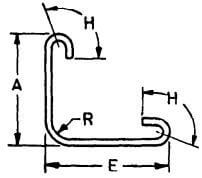A + E – 0.5 R – d + 2H		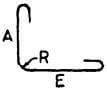A + E – 0.5 R – d + 18d	A + E – 0.5 R – d + 22d	A + E – 0.5 R – d + 26d
Q		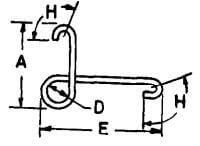A + E + 1.5 D + 2H		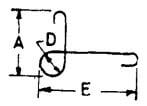A + E + 1.5 D + 18d	A + E + 1.5 D + 22d	A + E + 1.5 D + 26d
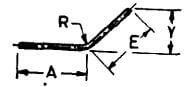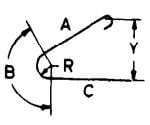
R		If angle with horizontal is 45^o or less A + E		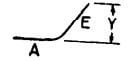A + E	A + E	A + E
S		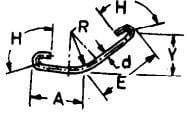If angle with horizontal is 45^o or less R is 12d or less A + E + 2H If the angle is greater than 45^o and R exceeds 12d, L to be calculated		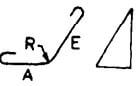A + E + 18d	A + E + 22d	A + E + 26d
T		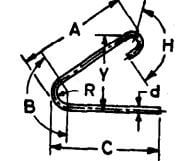If angle with horizontal is 45^o or less A + B + C + H -2(R + d) If the angle is greater than 45^o and R exceeds 12d, L to be calculated		A + B + C + 9d -2(R + d)	A + B + C + 11d -2(R + d)	A + B + C + 13d -2(R + d)
U		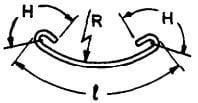L + 2H		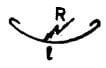L + 18d	L + 22d	L + 26d
V		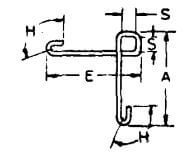A + E + 2S + 2H + d		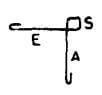A + E + 2S + 18d + d	A + E + 2S + 22d + d	A + E + 2S + 26d + d
W		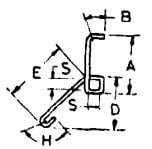A + E + 3S + 2d + B +H		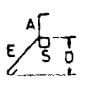A + E + 3S + 2d + 6d + 9d A + E + 3S + 17d	A + E + 3S + 2d + 7d + 11d A + E + 3S + 20d	A + E + 3S + 2d + 8d + 13d A + E + 3S + 23d
X		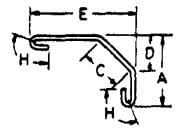A + E + C + 2H – √ ( C² – D² ) -D		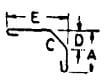A + E + C + 18d – √ ( C² – D² ) -D	A + E + C + 22d – √ ( C² – D² ) -D	A + E + C + 26d – √ ( C² – D² ) -D
Y		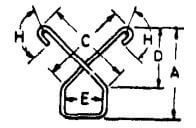E + 2(A – D + C + H)		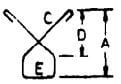E + 2(A – D + C + 9d)	E + 2(A – D + C + 11d)	E + 2(A – D + C + 13d)
Z		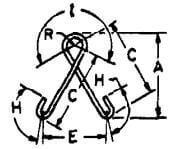L + 2C + 2H		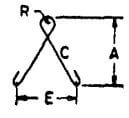L + 2C + 18d	L + 2C + 22d	L + 2C + 26d
AA		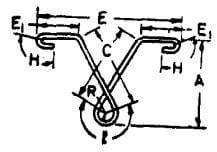2C + 2E1 + L + 2H		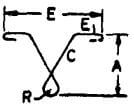2C + 2E1 + L + 18d	2C + 2E1 + L + 22d	2C + 2E1 + L + 26d
AB		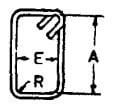2 (A + E) + 24d		2 (A + E) + 24d	2 (A + E) + 24d	2 (A + E) + 24d
AC		2 (A + E) + 20d		2 (A + E) + 20d	2 (A + E) + 20d	2 (A + E) + 20d
AD		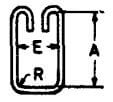2A + E + 28d		2A + E + 28d	2A + E + 28d	2A + E + 28d
AE		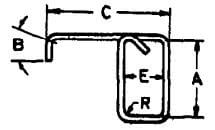2A + E + C +12d + B		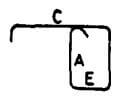2A + E + C +12d + 6d 2A + E + C +18d	2A + E + C +12d + 7d 2A + E + C +19d	2A + E + C +12d + 8d 2A + E + C +20d
AF		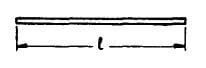L	Straight	L	L	L