Dynamic Vs Kinematic Viscosity (Difference & Definition)

What Is Viscosity?

Viscosity is a basic characteristic property of all liquids. When a liquid flows, it’s an inner resistance to flow. Viscosity is a measure of the resistance to flow or shear.

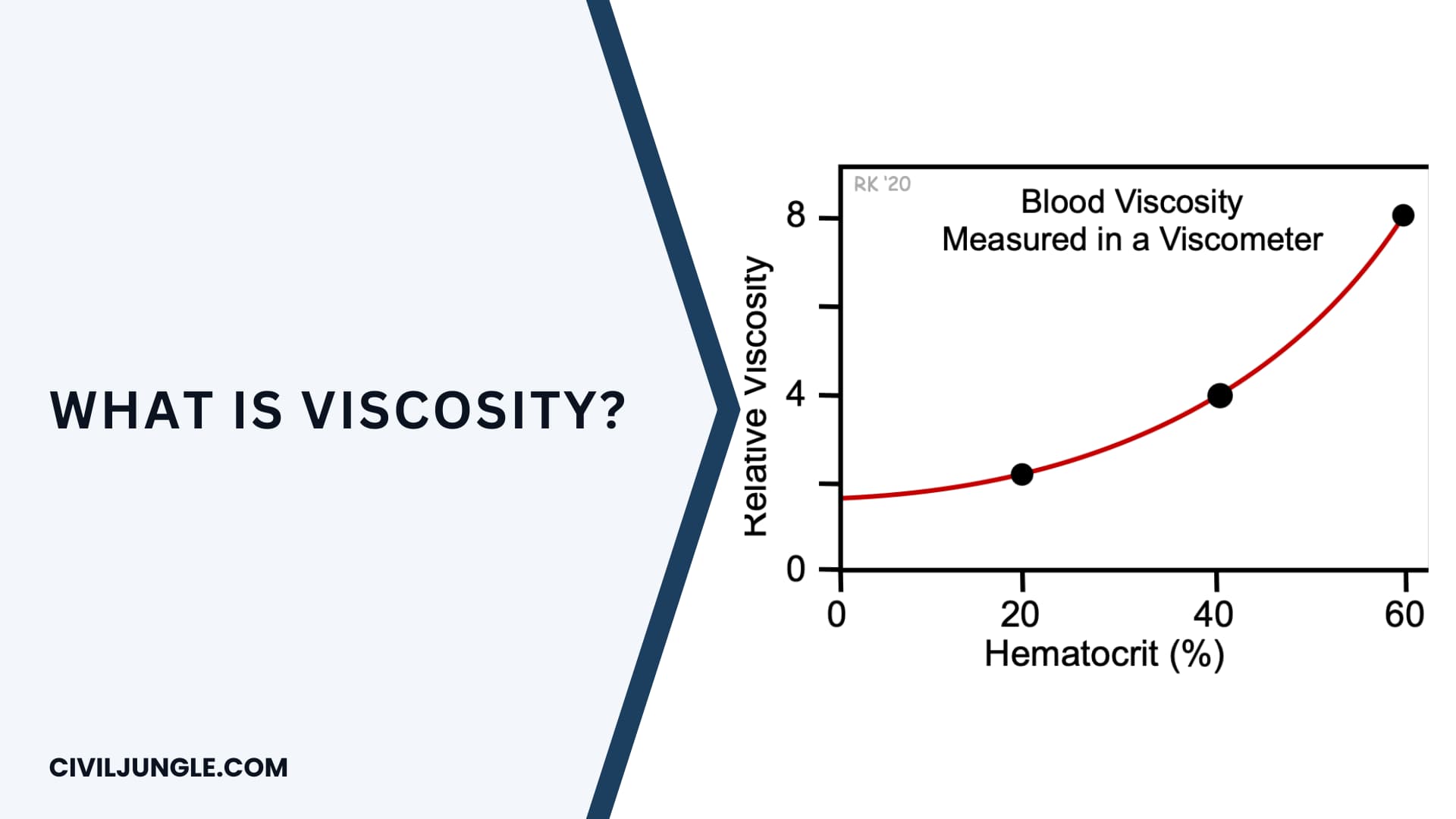
Viscosity may also be termed as a drag force and is a measure of the frictional properties of this fluid. Temperature and pressure function of Viscosity.

Though the viscosities of both liquids and gases vary with pressure and temperature, they affect the viscosity in another manner.

Within this book, we’ll deal primarily with a viscosity of fluids and its change as a function of temperature.

Viscosity is expressed in two distinct forms:

• Dynamic viscosity
• Kinematic viscosity

What is Dynamic Viscosity?

Dynamics of fluid flow is the study of fluid motion, including the forces causing flow. Viscosity (Dynamic) is defined as the resistance offered to a layer of fluid when it mores over another layer of fluid.

Rate of shear stress is directly proportional to the velocity gradient. Dynamic viscosity is flowed the newton 2nd Law (Second law) as per newton second law of motion. He says which relates the acceleration with the forces.

Due to the force exerted on the material, the deformation causes the fluid-fluid particle to move. Science ‘fluid’ Kinematics viscosity, studying only motion without thinking of force.

This chapter presents the first primary discussion of the science of fluid force fluid dynamics and its practical and general application.

A clear concept of force and acceleration is necessary to understand the speed of the transmission. According to Newton’s law of motion (Newton’s Second Law of Motion),

force (force) = Mass X Acceleration

f = m.a  (F=Force, M= Mass, A = Acceleration)

It is usually the practice of using m (Mass) in the pursuit of force for a solid. But the Greek letter p is used for fluid-fluid particulars.

Acceleration is used only for acceleration or for acceleration. The actual force applied to a particular solution according to Newton’s rule – net force, Its product of force and acceleration is equal to – product.

Thus the fluid has viscosity – viscosity. But to develop equations of motion, the equation is considered inviscid – inviscid.

In reality, no true view is devoid of real fluid. But other factors such as pressure force – pressure force and gravity force –
Since the viscous effect is insignificant relative to the gravitational force, it can be ignored, and in doing so, there is no possibility of major impairment.

One fact should be noted that in some cases, the force of prudence may also be important. For example, glycerin cannot be ignored when a fluid flows into a narrow tube or flows between two adjacent surfaces.

Since airtightness is extremely low in air motion, it can be easily ignored, but the fact that air is compressible cannot be ignored.

Assuming that the pressure of convection is caused by gravitational force, the equation can be written as follows (Dynamic Vs. Kinematic Viscosity).

Actual tension force on gravity + gravitational force = volume of force x its acceleration Net pressure force on a fluid particle + net gravity force on a fluid particle = particle mass x particle acceleration.

τ = µ x du/dy

• du/dy = constant of proportionality
• µ = Dynamic viscosity
• τ = Coefficient Euler’s equation of motio

Also read :What is Bulkage of Sand?

Equation of Motion

• Euler’s equation of motion

(1/p) x (dp/ds) = -v x (dv/ds)

• • p = Density of fluid
  • dA = Cross-sectional area of this fluid element
  • ds = Length of this fluid element
  • dW = Weight of this fluid element
  • P = Pressure on this element at A
  • P+dP = Pressure on this element at B
  • v = velocity of This fluid element

• Bernoulli’s equation from Real Fluid

P+(1/2).p.v.v +p.g.h = Constant

• • P = Pressure on the element at A
  • p = Density of fluid
  • v = Velosity
  • h = elvation
  • g = gravitational elevation

What Is Kinematic Viscosity?

Kinematic viscosity: Defined as the ratio of the dynamic viscosity (mass viscosity) of a fluid Mathematically,

Kinematic viscosity  ∝ = Dynamic viscosity (µ) / Density (δ)

• ∝ = Kinematic viscosity
• µ = Dynamic viscosity
• δ = Density

∝ = µ / δ

Topics related to acceleration and types of motion, etc. are discussed. An initial discussion of the equation for pressure and total force and pressure center due to the viscosity properties and the static mass.

It also moves due to a very small amount of learner stress on the visual. Likewise, the motion is also due to the slight imbalance in the membrane pressure on the visual.

Also, read: CONSISTENCY TEST OF CEMENT

Type of Kinematic Viscosity Flow:

1. Steady and unsteady flows.
2. Uniform and non-uniform flows.
3. Laminar and turbulent flows.
4. Compressible and incompressible flows.
5. Rotational and irrotational flows.
6. One, two, and three-dimensional flows.

1. Steady and unsteady flow:

Steady flow: the type of flow in which the fluid properties Remains constant with time.

u,v,w=0  dv/dt=0 dv/ds =0

• • dv= change of velocity
  • dt = time
  • ds = length of flow in the direction S

Unsteady flow: type of flow in which the fluid properties changes with time.

dv/dt ≠ 0  dv/ds =0

• • dv= change of velocity
  • dt = time
  • ds = length of flow in the direction S

Also, read : SOUNDNESS OF CEMENT TEST

2. Uniform and non-uniform flows:

Uniform flows A type of flow in which velocity pressures, density, temperature, etc. At only give time does not change with respects to scope.

dv/ds = 0, dp/ds = 0

• • dv = change of velocity
  • dt = time
  • ds = length of flow in the direction S

Non-Uniform: velocity, pressures, density, etc. at give time change with respect to space

dv/ds ≠ 0, dp/ds =0

Also, read : CORE CUTTER METHOD

3. Laminar and turbulent flows:

Laminar flow: Defined as that type of flow in which the fluid particles move along well-defined paths or streamline, and all the streamline is strength and parallel.

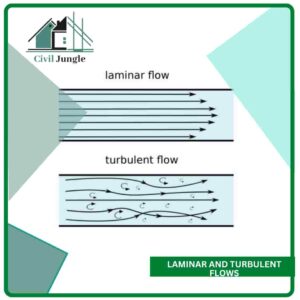
• Laminar flow is also called viscous flow or stream,
• This type of flow is only possible at slow speed and in a viscous fluid

Turbulent flow: in which fluid particles more irregularly and disorderly, i.e., fluid particles move in a zig-zag way. The zig-zag irregularly of fluid properties is responsible for high energy loss.

Also, read: IS CODE FOR CIVIL ENGINEER [Q&A]

4. Compressible and Incompressible Flows:

Compressible flow: Type of flow in which the density of the fluid changes from point to point or in other words, the density (p) is not constant for the fluid.

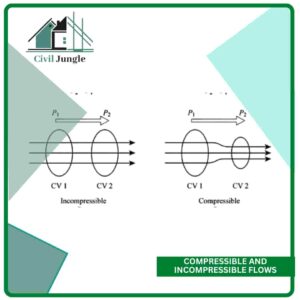
Thus, mathematically, for compressible flow

p  ≠ Constant

Incompressible flow: Type of flow in which the density is constant fluid flow. Liquids are generally incompressible then gases are compressible.

Mathematically, for incompressible flow

p = Constant.

Also, read : LAB TEST ON AGGREGATES AT SITE

5. Rotational and Irrotational Flows.

Rotational flow: that type of flow in which the fluid particles, while flowing along stream-lines, also rotate about their own axis.

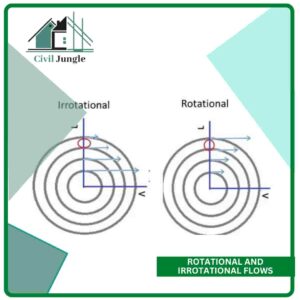
Irrotational Flows: Fluid particles while flowing along stream-lines, not rotate about their own axis then that type of flow is called irrotational flow.

Also read: PROCEDURE FOR RCC CONCRETE

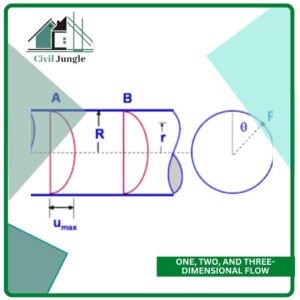
6. One, Two, and Three-Dimensional Flow:

One-dimensional:

• This is the flow in which the flow parameter such as velocity is a function of time, and one space co-ordinates only, say axis X.
• For a steady one dimensional flow in direction, the velocity is a function of one-space and co-ordinate only.
• The variant of velocities in additional two mutually perpendicular directions is assumed negligible.
• Hence mathematically, for one-dimensional

flow u =f( x), v = 0 and w = 0

• Where u, v and w are velocity components in x, y and z directions respectively.

Two-dimensional flow:

• That kind of flow in which the velocity is a function of time and two rectangular space co-ordinates say x and y.
• For a steady two-dimensional flow, the velocity is a function of two space coordinates only.
• The variation of velocity in that third direction is negligible.
• Thus, mathematically for two-dimensional flow

u = fi(x, y), v = f2(x, y) and w = 0.

Three-dimensional flow:

• That kind of flow where the velocity is a function of time and also three mutually perpendicular directions.
• However, to get a constant three-dimensional stream, the fluid parameters are functions of three space coordinates (x, y, and z) only.
• Thus, mathematically, for three-dimensional flow

u = fi(x, y, z), v = f2(x, y, z) and w = f3(x, y, z).