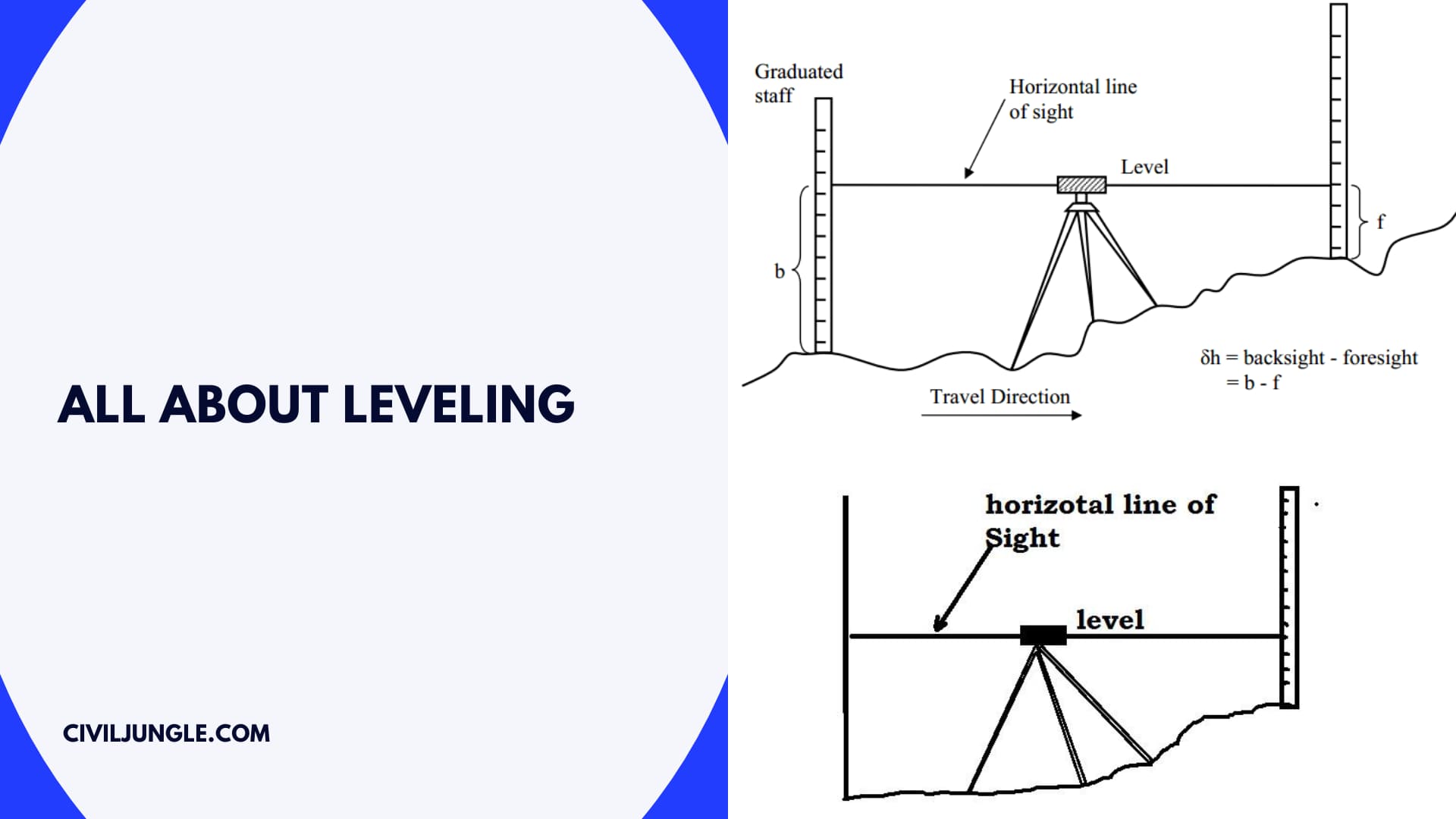
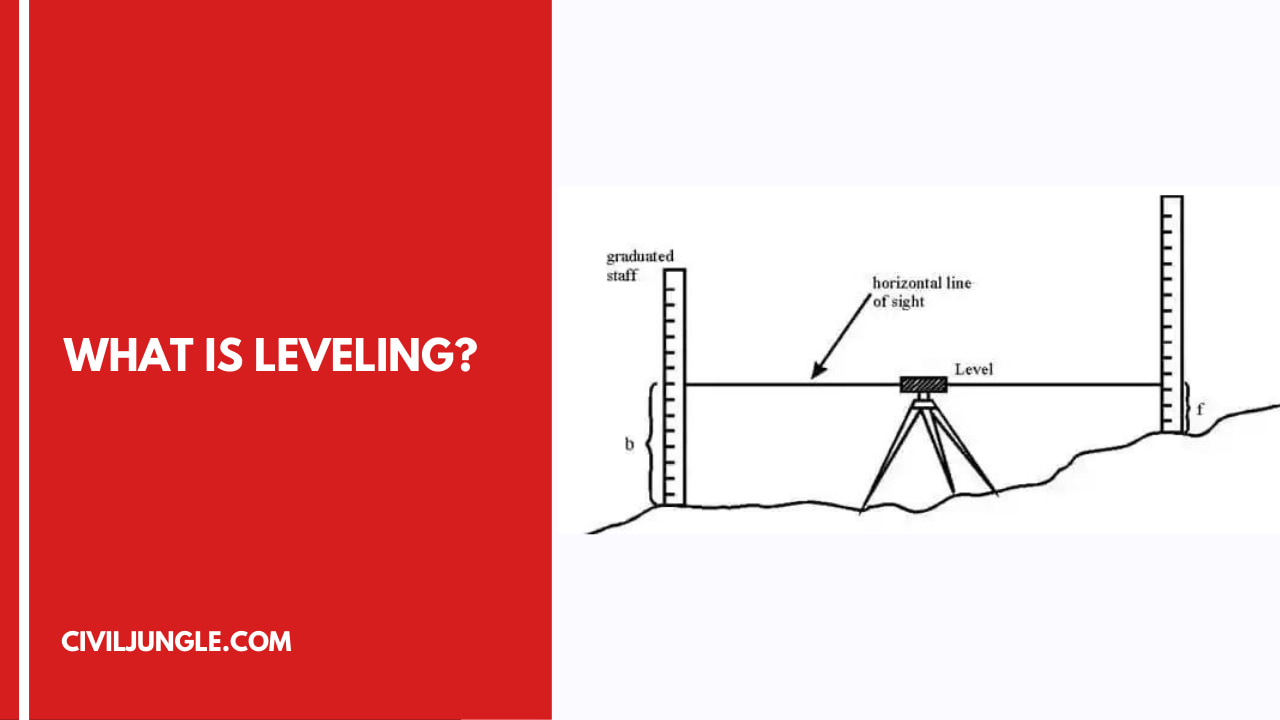
What Is Leveling?
Important Point
Leveling is the most widely used method for obtaining this elevation of ground points relative as a reference datum & is usually carried out as a separate procedure from that used for fixing a planimetric position.
Leveling involves the measurement of a vertical distance relative to a horizontal line of sight.
Therefore it requires a graduated staff for the vertical measurements and an instrument that will provide a horizontal line of sight.
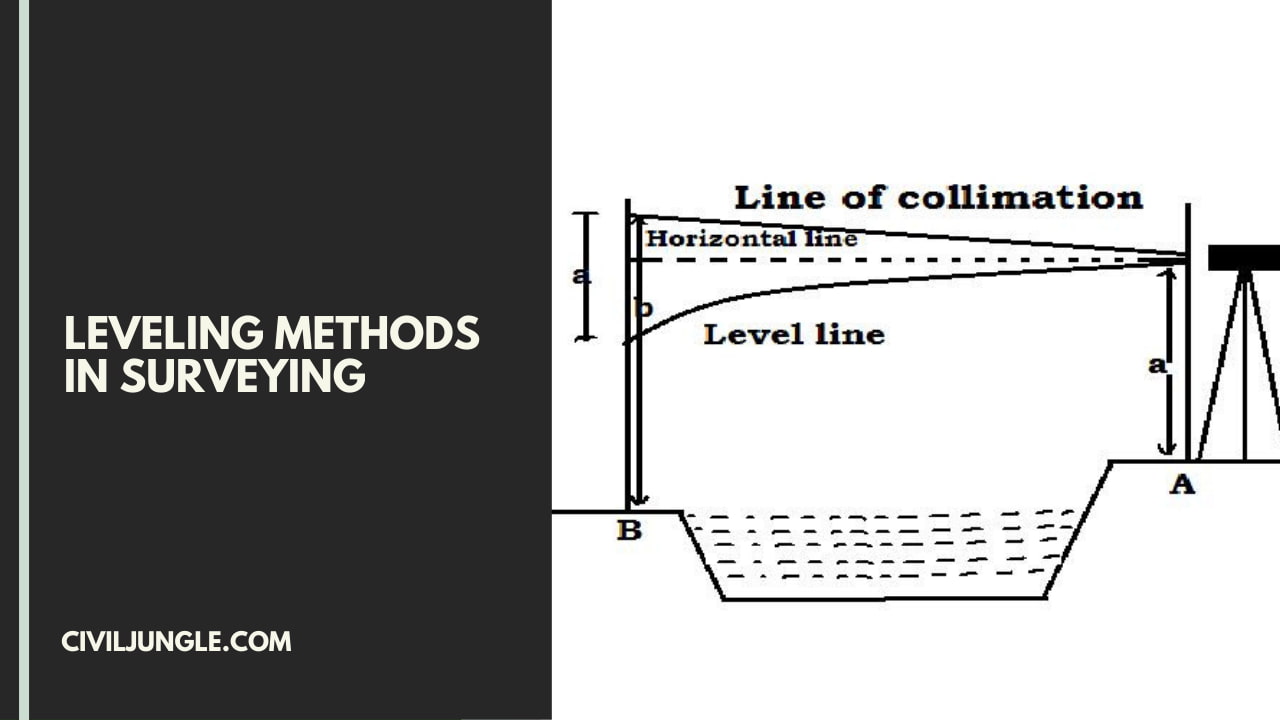
Leveling Methods in Surveying.
- Direct Leveling (Spirit Leveling)
- Barometric Leveling
- Hypsometric Leveling
- Stadia Leveling
- Indirect Leveling (Trigonometric Leveling)
Also, read: Benchmark in Surveying | TBM in Surveying | GTS Benchmark| Permanent Benchmark| Arbitrary Benchmark
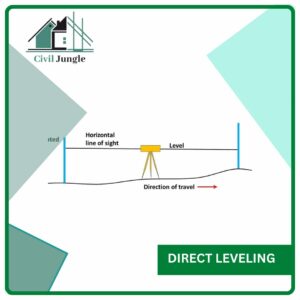
1. Direct Leveling (Spirit Leveling)
Direct leveling is a common form of leveling. In this method, the telescope is made horizontal, and the horizontality is checked using a spirit level.
Horizontal sight is taken on a graduated staff held at the point.
Reading helps in finding the difference in elevation.
Types of Direct Leveling
- Simple Leveling
- Differential Leveling
- Reciprocal Leveling
- Precise Leveling
- Fly Leveling
1.1. Simple Leveling
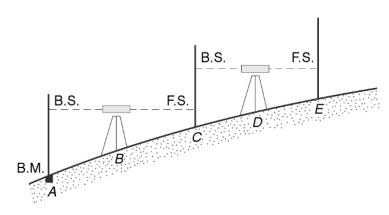
It’s the simplest operation in levelling when it’s necessary to locate the difference in elevation between two points, each of which is visible from a single position of the level.
The readings can be obtained on a staff held successively upon these points.
The precise situation of the level is immaterial, but to eliminate the instrumental error, the sight distances to the two staff positions should be kept as nearly equal as possible.
The level is set on a firm ground anywhere, not necessarily in the same vertical plane as that of the two staff positions.
Sampling leveling
Also, read: What Is EDM in Surveying | Type | Errors
1.2. Differential Leveling
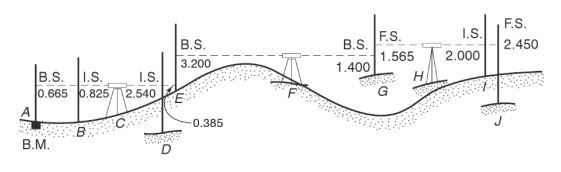
Determining this difference in elevation between two or more points without any regard to the alignment of the points is called differential leveling. It is used when:
- Two points are a large distance apart (as below fig -1)
- The difference in elevation between the two points is large (as below fig -2) and
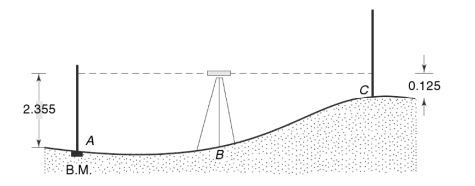
- Some obstacle intervenes between the points (as below fig-3)
Differential leveling (Point far apart) fig-1
Differential leveling (Point with large difference of elevation) fig-2
Differential leveling (Point having an obstacle in between ) fig-3
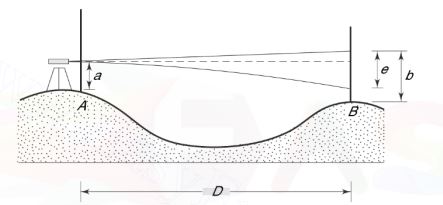
1.3. Reciprocal Leveling
It is the operation of leveling where the difference in elevation between two points is accurately determined by two sets of reciprocal observations.
This method is very useful when the instrument cannot be set up between the two points because of an obstruction such as a valley, river, etc., and if the sights are much longer than are ordinarily permissible.
For such long sights, the errors of reading the staff, the curvature of the earth, and the imperfect adjustments of the instrument become prominent. Special methods like reciprocal leveling should be used to minimize these errors.
Reciprocal Leveling
Also, read: Total Station in Surveying | Operations | Advantage & Disadvantage | Types
1.4. Precise Leveling
This is the operation of leveling in which precise instruments are used. In principle, there is no difference between ordinary and precise leveling.
In the former, the distances between checkpoints are relatively short, and the elevations obtained are satisfactory for routine purposes.
However, for precise leveling, the level loop may be of substantial length, and efforts are made to control all the sources of errors.
The most important error control in precise leveling is the balancing of foresight and backsight distances.
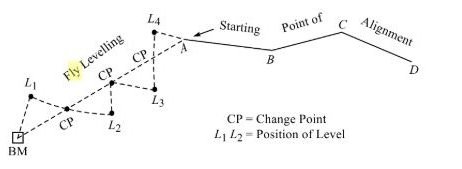
1.5. Fly Leveling
It is an operation of leveling in which a line of levels is run to determine the approximate elevations along a route. It is carried out for reconnaissance of linear structures such as roads, railways, tunnels, canals, etc.
Fly Levelling
Also, read: What Is Transit Theodolite | Theodolite Parts
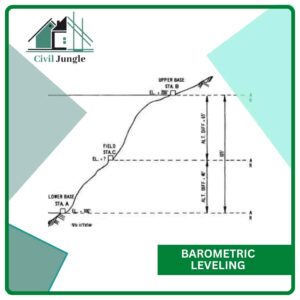
2. Barometric Leveling
The principle used in barometric leveling is that the elevation of a point is inversely proportional to the weight of the air column above the observer.
However, the relationship between pressure and elevation is not constant as air is compressible. Sudden changes in temperature, humidity, and weather conditions due to storms also affect the pressure.
The barometric methods are particularly suited for work in rough country, where high precision is not desirable. These are also used to reduce the slope distances to horizontal when measured electronically.
The instrument used for measuring pressure is called a barometer. The modified form of a barometer used to find relative elevations of points on the surface of the earth is called altimeter.
It is simple in operation but very sensitive to changes in atmospheric pressures. The method used to measure elevations with an altimeter is known as a single base method.
Two altimeters are required. One altimeter, along with a thermometer, is placed at a point of a known elevation called the control point, where the readings are taken at regular intervals.
The other altimeter, called roving altimeter, is taken to the points whose elevations are desired. Readings of the roving altimeter taken at the desired points are adjusted later in accordance with changes in temperature and the like observed at the control point.
The difference in elevation between the two points may be obtained by the following formula:
H = 18336.6 x (log10 h1 – log 10 h2) x (1+ ( (T1 + T2)/500))
H = The difference in elevation between the two points.
h1. h2 = The Barometric (in cm) at the lower and higher point respectively, &
T1.T2 =Tempratuers pf air (in 0C) at the lower and higher points respectively
Type of Barometric Leveling
- Barometer
- Mercurial Barometric
2.1. Barometer
Barometers are used in leveling for a rough determination of elevations, a difference of elevations, and the flying height of aeroplanes in aerial photogrammetry. They are also used for calculating the refraction correction in certain kinds of astronomical observations.
Since leveling with the barometer is not very accurate, it is normally used only for topographical and reconnaissance surveys on a small scale, where great accuracy in the determination of elevations is not essential.
Two kinds of barometers, the mercurial and the aneroid, are available (as per below fig.). The former is more accurate but is inconvenient to carry and breaks easily.
Barometer
| 1. Air-tight box | 2. Spring | 3. Central vertical post |
|---|---|---|
| 4. Knife edge | 5. Series of links | 6. Light chains |
| 7. Vertical spindle | 8. Hairspring | 9. Circular base plate |
| 10. Pointer | 11. Scale |
2.2. Mercurial Barometric
The Mercurial barometer depends on the principle of balancing a column of mercury against the atmospheric pressure, the atmospheric pressure at the point of observation being a function of the elevation of this point above mean sea level.
There are two main types of mercurial barometers—cistern and siphon. Mercurial barometers need to be supported vertically and are therefore often suspended by some form of gimbal mounting attached to a special tripod.
In the cistern type of barometer, the mercury is contained in a glass tube about 85 cm long, the upper end of which is closed, whereas the lower open end is immersed in a cistern containing mercury open to the atmosphere. The tube is exhausted of air so that the space above the level of the mercury in the tube is a vacuum.
Since the pressure on the mercury in the cistern is atmospheric and there is no pressure on the upper end of the column of mercury in the tube, a column of mercury is maintained in the tube; the height of which depends upon the pressure on the surface of the mercury in the cistern.
In the syphon type of mercury barometer, the tube containing mercury is bent into a U-shape at the lower end. One of the branches of the U-tube is kept shorter than the other.
A small opening is provided in the upper end of the short branch to admit air, while the long branch is closed at the top with the vacuum at its top. This type of barometer is inferior to the cistern type and is not much in use.
Also, read: Principle of Plane Table Surveying Methods |Equipment | Error | Advantage | Limitation
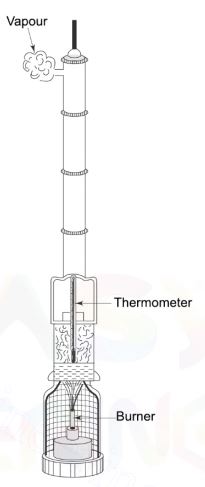
3. Hypsometric Leveling
The altitudes of various points may be obtained by using an instrument known as a hypsometer.
It works on the principle which a liquid boils when its vapor pressure is equal to the atmospheric pressure.
It may be noted that the boiling point of water is lowered as the pressure decreases, i.e., as a higher altitude is attained.
The method, therefore, consists in determining the boiling point temperatures at various stations.
The corresponding atmospheric pressures may be obtained from the tables. In the absence of tables, the following approximate formula may be used:
h = 76.00 ± 2.679 t
t is the difference of boiling point from 100°C, and It is the pressure in cm.
The difference in elevations may be obtained by using the formula given below formula.
H = 18336.6 x (log10 h1 – log 10 h2) x (1+ ( (T1 + T2)/500))
H = The difference in elevation between the two points.
h1. h2 = The Barometric (in cm) at the lower and higher point respectively, &
T1.T2 =Tempratuers pf air (in 0C) at the lower and higher points respectively
The hypsometer (as per above fig.) consists of a thermometer graduated to 0.1°C.
It is fitted inside a telescopic tube and is suspended over a small boiler filled with distilled water.
The thermometer is kept in steam and is adjusted so as not to touch the water.
The temperature of this air in the shade is also observed simultaneously with a detached thermometer.
4. Stadia Leveling
It is also known as Tacheometric Surveying. This common method of measuring horizontal distances is chaining, and that for measuring vertical distances is differential leveling.
Both of these methods give results to the required accuracy. Chaining, however, on rough grounds does not furnish very accurate results. When the ground is rough and more observations at a faster rate with ordinary precision are acceptable, then the tachometer is the choice.
An example of the use of a tachometer for the above-said conditions is the collection of data to draw contours on a topographic map. As compared to chaining on flat grounds, the accuracy of tachymetric distances is low, but on rough and steep grounds, the accuracy is more.
A tachometer is defined as an optical distance measurement method. Though less accurate, this method of surveying is very rapid and convenient.
The other names given to the tachometer are tachymetry or telemetry. The primary object of a tachymetric survey is the preparation of a contoured plan.
It is particularly suitable for filling at details on topographical maps, preliminary location surveys (e.g., for railways, roadways, canals, reservoirs, etc.) and surveying steep grounds, broken boundaries, and water stretches, etc.
Also, on surveys of higher accuracy, it may be used to provide a ready check on distances measured with a chain or tape. A tachometer is essentially a transit theodolite, the diaphragm of which is furnished with stadia wires in addition to the cross-wires.
Observations are made on stadia rod, usually a level staff but with a larger least count (1 cm), and horizontal as well as vertical distances are computed from these observed readings.
Stadia digraph
Also, read: What Is Traversing in Surveying | Types | Method | Definition
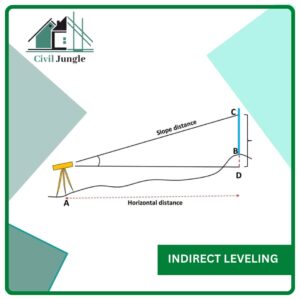
5. Indirect Leveling (Trigonometric Leveling)
This is an indirect method of leveling in which the difference in elevation of the points is determined from the observed distances measured and vertical angles.
The vertical angles are measured with transit, and the distances are measured directly or computed trigonometrically. Trigonometrical leveling is commonly utilized in topographical work to find out the elevation of the top of buildings, chimneys, church spires, etc.
Also, it may be used to its advantage in difficult terrains like mountainous areas. Depending on the field conditions and the measurements which may be made with the instruments available, there may be innumerable cases.
An attempt has been made to solve a few cases, and many more can be solved by the reader himself.
Also Read: Leveling Survey
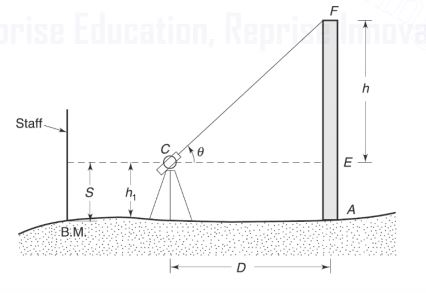
5.1. The base of the Object Accessible—The Object may be Vertical or Inclined
In as per below fig., AF is the vertical object, D is the horizontal distance between the object and instrument, S is the reading on the leveling staff held vertical on the B.M., h1 is the height of the instrument, h is the height FE, and θ is the angle of elevation on the top of the object.
Reduce the level of the top of a vertical object
- From triangle CEF,
- EF = CE tan θ
- h = D tan θ
- Reduced Level of F = R.L of B.M. + S +h
- Reduced Level of F = R.L of B.M. + S + D tan θ
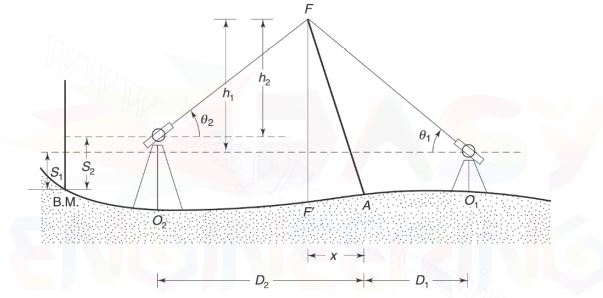
In as per below fig., AF is the inclined object, x is the distance between the foot of the object and the projection F’ of the top, O1 and O2 are the instrument stations such that O1, O2 and A are in the same vertical plane, D1 and D2 are the distances of the foot of the object from the instrument stations O1 and O2, respectively.
S1 and S2 are the staff readings on B.M. from instrument positions at O1 and O2, respectively, and θ1 and θ2 are the angles of elevation from O1 and O2, respectively.
Reduce the level of the top of an inclined object
Reduced Level of F = R.L of B.M. + S1 +h1
Reduced Level of F = R.L of B.M. + S + (D1 + x) tan θ 1
Reduced Level of F = R.L of B.M. + S1 +h1
Reduced Level of F = R.L of B.M. + S + (D2 – x) tan θ 2
x = ( S2 – S1 ) + D2 tan θ2 – D1 tan θ1 / tan θ1 + tan θ2
Also, read: What is Chain Surveying (Principal, Procedure, Method, Instrument)
5.2. The base of the Object Inaccessible—The Instrument Stations and the Elevated Object are in the Same Vertical Plane
When the horizontal distance between the instrument and the elevated object is inaccessible, the observations are made from two instrument stations. Assuming the two instrument stations and the object to be in the same vertical plane, the following two cases arise.
5.2.1. Instrument Axes at Same Level
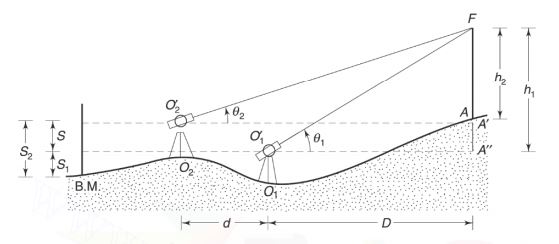
In as per below fig, h is the vertical distance FA’, S is the staff reading on the B.M., θ1 and θ2 are the angles of elevation from the instrument stations O1, and O2 respectively, D is the horizontal distance between O1 and the object, and d is the horizontal distance between the two stations.
h = D tan θ1
h = (D + d) tan θ2
Reduced Level of F = R.L. of B.M. S + h
D = d tan θ2 / (tan θ1 – tanθ2 )
5.2.2. Instrument Axes at Different Level
Depending upon the terrain, three cases arise:
- Instrument axis at O2 higher than that at O1
- Instrument axis in O1 higher than that at O2
- Instrument axes at very different levels
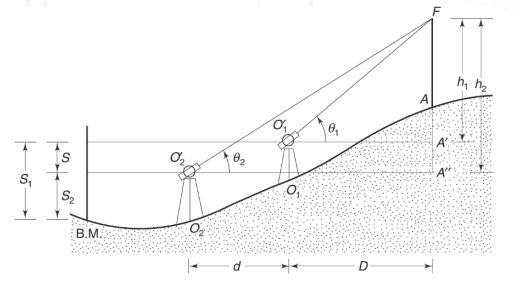
5.2.2.1. Instrument axis at O2 higher than that at O1 (as per below fig.)
h1 – h2 = S2 – S 1 = S
From triangle O1′ A” F, h1 = D tan θ1
From triangle O2′ A” F, h2 = (D + d) tan θ2
Reduced Level of F = R.L. of B.M. S1 + h1
D = (S+ d tan θ2) /(tan θ1 -tan θ2)
5.2.2.2. Instrument axis in O1 higher than that at O2
h2 – h1 = S1 – S 2 = S
From triangle O1′ A” F, h1 = D tan θ1
From triangle O2′ A” F, h2 = (D + d) tan θ2
Reduced Level of F = R.L. of B.M. S1 + h1
D = (d tan θ2 – S) /(tan θ1 -tan θ2)
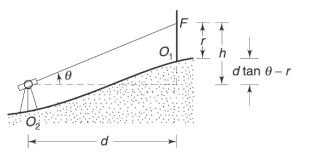
5.2.2.3. Instrument axes at very different levels (as per below both fig. )
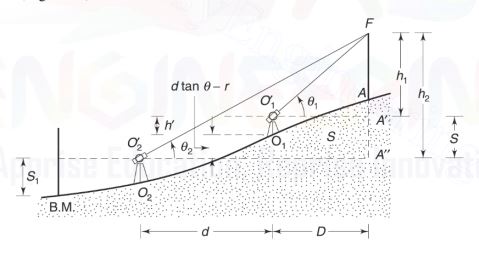
If the difference at elevation (S2 – S1) between the two instrument stations is too large and cannot be measured on staff at the B.M., then the following procedure is adopted:
Set up this instrument at O1 and measure the vertical angle at point F (as per below fig.).
Transit the telescope and establish a point O2, at a distance d from O1.
Shift this instrument to O2 and measure the vertical angle at point F.
Observe the staff reading r with respect to horizontal cross-wire on the staff at O1 (as per below fig). Let S be the difference at a level between the two axes in O1 and O2.
S = h2 – h1
D = ( d tan θ2 – S) / ( tan θ1 – tan θ2 )
Reduced Level of F = R.L. of B.M. S1 + s + h1
Reduced Level of F = R.L. of B.M. S1 + d tan θ – r + h’ +h1
Methods of Levelling
- Direct Leveling (Spirit Leveling)
- Barometric Leveling
- Hypsometric Leveling
- Stadia Leveling
- Indirect Leveling (Trigonometric Leveling)
Fly Levelling
Fly levelling is a very approximate form of levelling in which sights are taken as large. as possible. In this method a line of levels is run to determine approximately reduced levels. of the points carried out with more rapidly and less precision.
Reciprocal Levelling
Surveying leveling between two widely separated points in which observations are made in both directions to eliminate the effects of atmospheric refraction and the curvature of the earth.
Height of Instrument Method
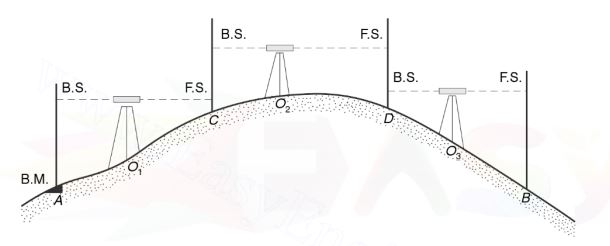
Height of instrument method deals with obtaining the RL of the line of collimation by adding BS reading of a point whose RL is known. The RL of line of collimation is called Height of Instrument. From this, the staff readings of all intermediate stations is subtracted to get the RL at those points.
Trigonometric Levelling
Trigonometric Leveling is the branch of Surveying in which we find out the vertical distance between two points with the help of some measurements of the vertical angles and the known distances. The known distances are either assumed to be horizontal or the geodetic lengths at the mean sea level(MSL).
Levelling Surveying
Levelling is a process of determining the height of one level relative to another. It is used in surveying to establish the elevation of a point relative to a datum, or to establish a point at a given elevation relative to a datum.
Fly Levelling Procedure
Fly leveling is conducted when the benchmark is very far from the work station. In such case, a temporary bench mark is located at the work station which is located based on the original benchmark. Even it is not highly precise it is used for determining approximate level.
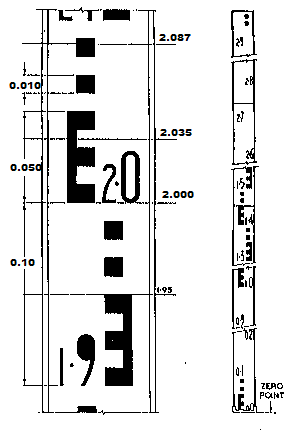
Levelling Staff Reading Method
To read the staff, take the number shown below the reticle. Count the number of whole 10mm increments between the whole number and the reticle. Then estimate the number of mm between the last whole 10mm block and the centre of the reticle. The diagram above shows 4 readings:- 1.950, 2.000, 2.035 and 2.087.
Leveling Survey
Leveling is a branch of surveying in civil engineering to measure levels of different points with respect to a fixed point such as elevation of a building, height of one point from ground, etc.
What Is Levelling in Surveying?
Leveling is a process to determine the vertical position of different points below, on, or above the ground. In surveying operations, vertical elevations and vertical control are generally derived independently of horizontal control.
Surveying and Leveling
Levelling is a process of determining the height of one level relative to another. It is used in surveying to establish the elevation of a point relative to a datum, or to establish a point at a given elevation relative to a datum.
What Is Levelling?
Levelling or leveling is a branch of surveying, the object of which is to establish or verify or measure the height of specified points relative to a datum.
Types of Levelling
Direct Leveling
- Simple leveling.
- Differential leveling.
- Fly leveling.
- Profile leveling.
- Precise leveling.
- Reciprocal leveling.
Simple Levelling
It is a simple and basic form of leveling in which the leveling instrument is placed between the points which elevation is to be find. Leveling rods are placed at that points and sighted them through leveling instrument.
Levelling in Civil Engineering
Levelling is the art of determining the relative elevations of different objects or points on the earth’s surface. This is done by taking measurements in the vertical plane. Hence, this branch of surveying deals with measurements in vertical planes.
Methods of Levelling a Building Site
What are the main levelling methods?
- direct levelling , where you measure differences in elevation directly. This is the most commonly used method;
- indirect levelling , where you calculate differences in elevation from measured slopes and horizontal distances.
Classification of Levelling
In the case of agricultural engineering, there are eight types of levelling as “different levelling”, “check levelling”, “profile levelling”, “cross-sectioning”, “reciprocal levelling”, “barometric levelling”, “hypsometry”, and “trigonometric levelling”.
Differential Levelling Is Also Known as
Total Station differential levelling (also known as trigonometric heighting) is a variant of conventional differential levelling. Differences in height can be determined by making a series of zenith angle and slope distance observations to a prism mounted on a fixed height pole.
Barometric Levelling in Surveying
In barometric leveling, differences in height are determined by measuring the differences in atmospheric pressure at various elevations. Air pressure is measured by mercurial or aneroid barometer, or a boiling point thermometer.
Indirect Levelling
Indirect leveling, also known as barometric leveling or hypsometry, is a method used in surveying and geodesy to determine the difference in elevation between two points. Unlike direct leveling, which relies on the use of leveling instruments and measuring staffs, indirect leveling utilizes atmospheric pressure measurements to estimate the height difference.
Barometric Levelling
Barometric leveling, also known as barometric altimetry or barometric surveying, is a method used to determine the difference in elevation between two points by measuring the atmospheric pressure at those locations. It is commonly employed in situations where direct leveling methods are impractical or time-consuming.
Simple Leveling
The operation of levelling for determining the difference in elevation, if not too great between two points visible from single position of the level is known as simple levelling.
Method of Levelling in Surveying
There are three leveling techniques: differential, trigonometric, and barometric. Differential leveling is the most accurate of the three methods. With the instrument locked in position, readings are made on two calibrated staffs held in an upright position ahead of and behind the instrument.
What Is Fly Levelling?
Fly levelling. it is a very approximate form of levelling in which sights are taken as largeas possible. In this method a line of levels is run to determine approximately reduced levelsof the points carried out with more rapidly and less precision.
Levelling Process
The leveling process is a surveying technique used to determine the height differences or elevations between various points on the Earth’s surface. It is commonly employed in construction, civil engineering, and land surveying to establish accurate horizontal and vertical control.
Like this post? Share it with your friends!
Suggested Read –
- Types of Tunnel
- What Is Lintel | Type of Lintel
- What Is EDM in Surveying | Type | Errors
- Top 10 Best Cement Companies In India 2021
- Difference Between Plinth Level, Sill Level, and Lintel Level.
- What Is Honeycomb In Concrete | Cause | Cure | Type of Grouting
- What Is Development length | What Is Development Length of Bars
- 14 Difference Between One Way Slab and Two Way Slab | What is Slab | What Is a One Way Slab




Leave a Reply