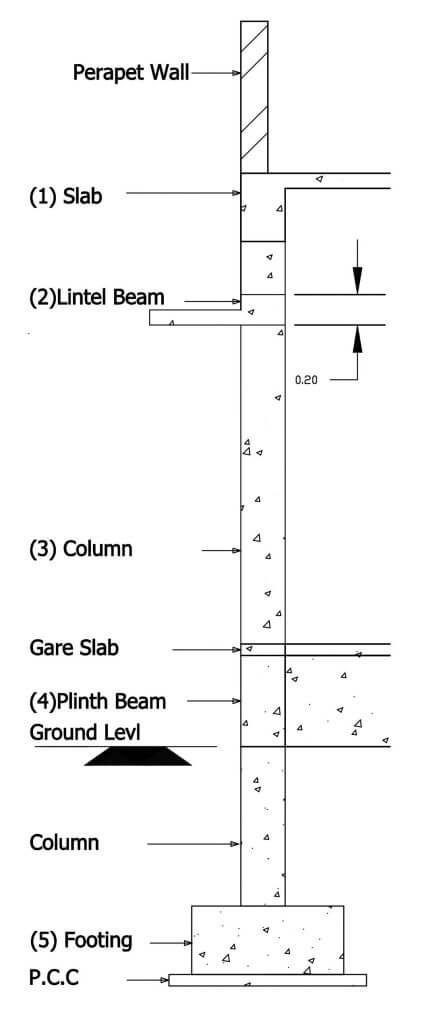
Any construction building design as per the below step. In this article, we design only slab and next article next steps calculation.
(1) Slab Design
(2) Slab Beam Design
(3) Lintel Beam Design
(4) Column Design
(5) Plinth Beam Design
(6) Footing Design
Some Important Point for Slab Design
Type of Slab
A slab is a plate element having a depth (D), Very small as compared to its length and width slab is used as floor or roof in building, carry uniformly distributed load.
Slab may be
- Simply Supported
- Continuos
- Cantilever
Type of Slab Based on Support Conditions Are:
1). One Way Spanning Slab
2). Two Way Spanning Slab
3). Flat Slab Resting Directly on Columns Without Beams
4). Grid Slabs or Waffle Slabs
5). Circular Slab and Other Shapes
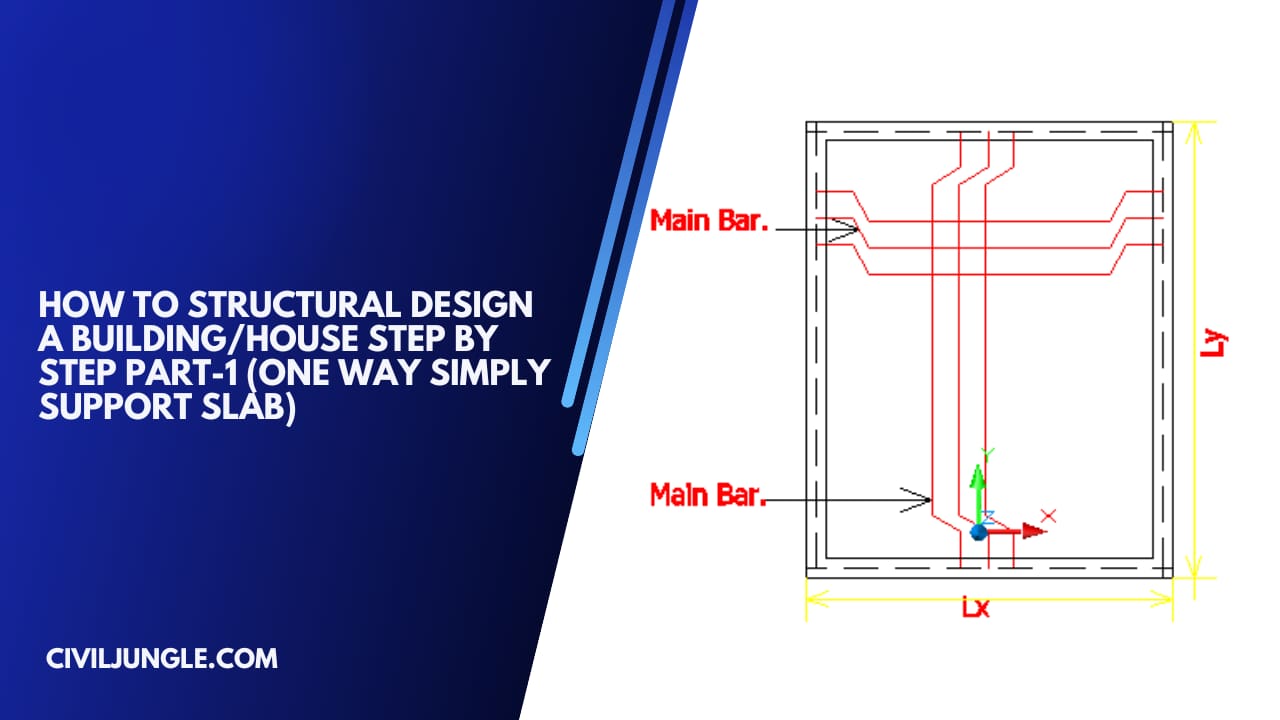
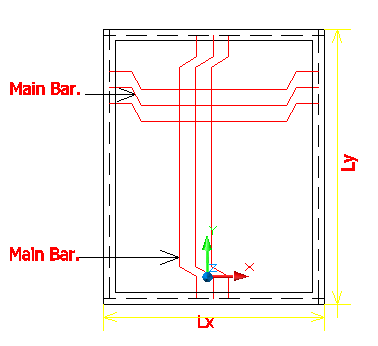
One Way Spanning Slab
If the slab is supported on two opposite sides. it is called a one-way spanning slab. In this type of slab, lads are transferred on two opposite supports as shown below figure.
One Way Slab
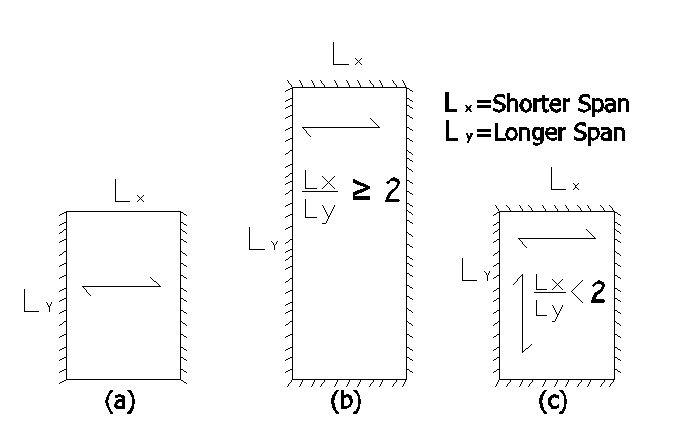
If the slab is supported on four sides, and if ly/lx ≥ 3 one way spaning slab.
For any slab, if ly = lx, the slab has a tendency to bend in both the directions Which increase is provided along lx (Short Span)
Two Way Spanning Slab
It the slab is supported on all four edges and if ly / lx < 2,
The tendency of the slab is to bend in both directions. Such slabs are called a two-way slab. ( as shown below figure.)
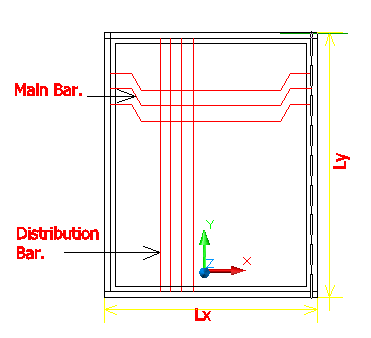
In a two-way slab, the main reinforcement is provided along with lx as well as ly direction.
Flat Slab
When the slab is directly supported on columns, without beams, it is known as a flat slab.
Flat slabs are provided to increased the floor height and to permitted a large amount of light which might be obstructed by the depth of beams.
Grid Slabs
When the slab is required on beams with columns only on the periphery of the hall, the slab is called grid slab
Sometimes, in a large hall, public places, marriage halls, auditoriums, etc. a large column-free area is required. In these cases, large deep beams may be permitted but the columns are permitted only on the periphery
One Way Simply Support Slab Calculation /Design
One Way Simply Support slab Below Point Calculation Required
1. Effective Depth (d)
2. Effective Span
3. Reinforcement Requirements
4. Check for Cracking
5. Check for Deflection
6. Check for Development Length (Ld)
Effective Depth (d)
For deflection control
L/d = 20 X M.F
- M.F. Modifiction factor from— IS: 456, p.38.Fig-4
- Assume % steel 0.3 to 0.6%
Fs = 0.58 Fy X (Ast requierd / Ast Provied)
Initially assume that Ast reqierd = Ast Provided
Fy = 250 N/ Sq.mm —– Fs = 0.58 X 250 = 145 N/ sq.mm.
Fy = 415 N/ Sq.mm —– Fs = 0.58 X 415 = 240 N/ sq.mm.
Fy = 500 N/ Sq.mm —– Fs = 0.58 X 500 = 290 N/ sq.mm.
Effective Span
Clear Span + d
c/c of Supports
Whichever is smaller ——– as per IS 456-2000 P. 34, CI 22.2.a
Reinforcement Requirements
Minimum reinforcement
For Fe-250 Pt = 0.15 % of total C/s area (d x D)
For Fe-415 Pt = 0.12 % of total C/s area (d x D)
For Fe-500 Pt = 0.12 % of total C/s area (d x D) ——– as per IS 456-2000 P. 48, CI 26.5.2.1
Maximum diameter (Sp 34)
For minbar:
- Plain bars———–10 mm Ø min dia
Deformed bars—–8 mm Ø min dia
For Distribution bars:
- Plain bars———–6 mm Ø min dia
Deformed bars—–6 mm Ø min dia
Check for Cracking
For Min Steel:
3d ——— Where. d = Effective depth
300 mm
Spacing should not exceed smaller these two values.
For Distribution steel:
5 d
450 mm
Spacing should not exceed smaller these two values. ——- IS: 456-2000, P.46
Check for Deflection
Allowable L/d = 20 X M.F.
- M.F is Obtained from IS:456-200 P-38 Fig 4
Find actual, L/d
If Actual L/d < allowable L/d ———- Ok
Check for Development Length (Ld)
IS 456-2000,P.44, Cl. 26.2.3.3 C
Ld should be ≤ 1.3 (M1/V) + L0
Where
Ld = (Ø.σs / 4 τ bd )—————–σs = 0.87 fy As per IS 456-200, P.42
50 % of steel is bent up near support. Therefore find M.R for 50 % of steel only
M1 = M.R. for 50% steel support
V = Shear force at the support
L0 = Sum of anchorage beyond the center of support
d
12 Ø
Take L0 as the smaller of two values.
One Way Simply Support SlabCalculation /Design- Example
Sum Point Consider As below
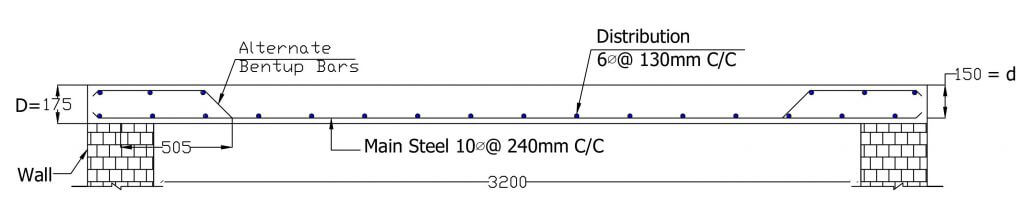
Slab Size 3.2m X 9.2 m
The slab is resting on 300mm thick wall
Find One Way Slab or Two Way Slab
ly/lx = 9.2 / 3.2 = 2.875 > 2
As per the type of slab
Here this one-way slab, So we design the slab as one-way simply supported slab
Effective Depth (d)
Here Consider shorter span as l,
l = 3200 mm = 3.2 m
l/d = 20 x M.F
fy – 415 N/sq.mm, fs = 240 N / Sq.mm
M.F = 1.15 | As per IS Code 456, Fig.4
l/d = 20 x 1.15
3200/d = 20 x 1.115
d = 139.13 mm
Here, d = 150 mm , Assume 10 mm Ø bars
Overall Depth, D = 150 + (Ø / 2 ) + Clear Cover
D = 175 mm
Effective Span
1). 3200 + 150 = 3350 mm
2). c/c of Supports = 3200 + 300 = 3500 mm | IS: 456-2000,P-34, CI. 22.2.a
Whichever is smaller
Effective Span = l = 3350 mm = 3.35 m.
Reinforcement Requirements
Load Calculations
| Dead load | 4.375 | Kn/m |
| Floor Finsh | 1 | Kn/m |
| Live Load | 2.5 | Kn/m |
| Total Load | 7.875 | Kn/m |
Factored Load = 1.5 x 7.875
w = 11.82 kn/m.
Bending Moment
Mu = (w. l2) / 8 = (11.82 / 3.352)
Mu = 16.58 Kn.m.
Main Steel
Pt = 50 (fck/fy) [1 – √ ( 1 -{(4.6 Mu)/ (fck x bd2)})]
Pt = 50 x (0.482) x (0.0945)
Pt = 0.215 %
Ast = ( pt / 100) x 1000 x 150
Ast = 322.5 mm2
For Spacing
Sapcing = ({[π/4] x d2}/Ast ) x 1000 mm
Sapcing = ( 78.53 / 322.5 ) x 1000 = 243.50 mm
Distrbution Steel
Provide a minimum of 0.120% of Total C/s Area | As per IS 456-200 P 48, CI. 26.5.2.1
Ast = (0.12/100) x 1000 x 175 = 210 Sq.mm
Check for Cracking
For Main Steel
1). 3 d = 3 x 150 = 450 mm
2). 300 mm | IS 456-2000 P-46
240 mm provided < 300 mm …………….. o.k.
For Distribution Steel
1). 5 d = 5 x 150 = 750 mm
2). 450 mm
130 mm provided < 450 mm …………….. o.k.
Check for Deflection
Allowable (l/d) = 20 x M.F.
% pt Provided = 100 Ast / bd = (100 x 327) / (1000 x 150) = 0.218% | IS Code 456-2000 P.38, Fig 4
M.F = 1.6
Allowable l/d = 20 x 1.6 = 3350 / 150 = 22.33
22.33 < 32 …………….. o.k.
Check for Development Length (Ld)
1). d = 150 mm
2). 12 Ø = 12 x 10 = 120 mm
Taking larger of two values L0 = 150 mm
S.F. at support = 50% of East at mid-span = 327 / 2 = 163.5 Sq.mm
M1 = 0.87 x 415 x 163.5 x 150 x [1-(415 x 163.5) / (20 x 1000 x 150)]
M1 = 8.65 x 106 N.mm = 8.65 kN.m.
1.3 [ M1/V] + L0 = 1.3 x (8.65 x 106 ) / (18.91 x 103 ) + 150
M1 = 744.65 mm
for M 20 , fy = 415 N/mm2
10 mm Ø. bar, tension
Ld = 470 mm
470 mm < 744.65 mm …………….. o.k.
Reinforcment Details
One Way Simply Support Slab Calculation /Design Excel Sheet – Download
Video tutorial for better understanding:
Like this post? Share it with your friends!
Suggested Read –
Leave a Reply