What Is Slab?
Important Point
A slab is constructed to provide flat surfaces, typically horizontal, in building roofs, floors, bridges, and other types of structures. The slab could be supported by walls, by reinforced concrete beams normally cast monolithically with the slab, by structural steel beams, either by columns or from the ground.
A slab is a plate element having depth (D), very small as compared to its length and width. A slab is used as floor or roof in buildings, carry distribution load uniformly.

Type of Slab b
Slab May Be
- Simply Supported
- Continuos
- Cantilever
Also, read: What Is a Bar Bending Schedule | Preparation as Per Bs 4466 | Tolerances as Per Bs 4466
Type of slabs based on support conditions are:
- One Way Slab
- Two Way Slab
- Flat Slab Resting Direction on a Column Without Beam
- Grid Slabs or Waffle Slab
- Circular Slab and Other Shapes
Also, Read: Waffle Slab Design
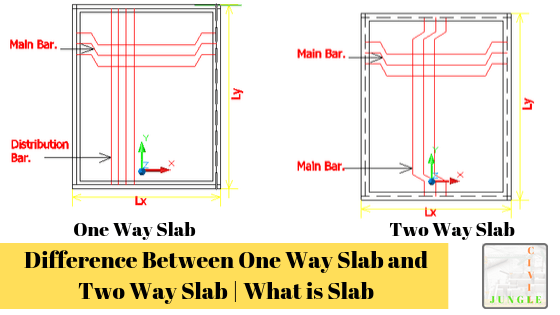
What Is a One Way Slab?
According to IS 456:2000, The ratio of longer span(l) to shorter span(b) which is (L/B) greater than 2 is known as One way slab. In practical, One way slab is supported by only two parallel beams or walls. Normally we don’t use one way slabs often.
or
One Way Slab
The most straightforward routine structural element for illustration of design provisions from the Code is that the one way slab.
A one way slab is defined for functions of the book as a flexural member with thickness small relative to other dimensions, supporting (gravity) loads applied normal to and directly above its surface, a span in one direction between parallel supports, and fortified for flexure in this direction only.
For purposes of analysis, one way slabs might be restrained to some degree in the supports or possibly unrestrained. A number of Code provisions reference to “flexural members,” including one and two way slabs, beams, girders, footings, as well as where bending is present together with the axial walls, load, and columns.
In general, when this code provision is intended to use to one way slabs, the term is going to be utilized in the sense of this definition herein.
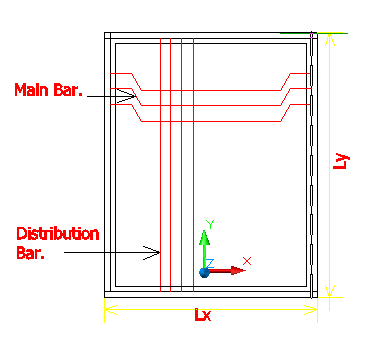
If the is supported on two opposite sides, it is called a one way spanning slab. In this type of slab, loads are transferred on two opposite as per the above figure. A
If the slab is supported at four sides, and if Ly/Lx ≥ 2 one way spanning slab.
For any slab, if Ly = Lx, the slab has a tendency to bend in both directions. With an increase of Ly, the tendency of bending along Ly is reduced and that on Lx is increased.
When Ly/Lx ≥ 2, the slab bends only in X directions
When Ly/Lx ≥ 2, the slab is called a one way slab. In one way slab, the main reinforcement is provided along Lx ( Short Span)
Also, read: Total Station in Surveying | Operations | Advantage & Disadvantage | Types
What Is a Two Way Slab?
A two way street is a street that allows vehicles to travel in both directions. On most two way streets, especially main streets, a line is painted down the middle of the road to remind drivers to stay on their side of the road. Sometimes one portion of a street is two way and the other portion is one way.
or
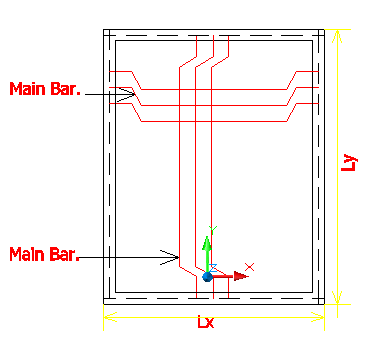
The design considerations of wall supported two way slabs are similar to those pertaining to one way slabs.
The thickness of the slab is generally based on deflection control criteria, and the reinforcements in the two orthogonal directions are designed to resist the calculated maximum bending moments in the respective directions at the critical sections. [Additional reinforcement may be required at the corners of two way slabs in some cases, as explained later].
The slab thickness should be sufficient against shear, although shear is usually not a problem in two way slabs subjected to uniformly distributed loads.
If the slab is supported at all four edges and if Ly/Lx < 2,
The tendency of the slab is to bend in both directions. Such slab is called two way slab as per above figure c
In two way slabs, main reinforcement is provided along Lx as well as Ly direction
Also, read: Principle of Plane Table Surveying Methods |Equipment | Error | Advantage | Limitation
What Is the Flat Slab?

Flat Slab
When the slab is directly supported on a column, without beams, it is known as a flat slab.
Flat slab is provided to increase the floor height and to permit a large amount of light which might be obstructed by the depth of beams.
What Is Grid Slab?
Grid Slab
When the slab is supported on beams with column only on the periphery of the hall, the slab is called grid slab. Sometimes, in large halls, public places, marriage halls, auditoriums, etc. a large column free area is required.
In these cases, large deep beams may be permitted, but the columns are permitted only on the periphery.
Also, read: Procedure For Rcc Concrete
Analysis of Slab:
Slabs are primarily flexural members as beam and are analyzed and designed in the same manner as the beams. The analysis may be carried out as follows:
Elastic Analysis:
A strip of 1 m width of the slab is considered, and loads are found on this strip. This strip id analyzed as a beam 1 m width.
Code Coefficients:
This is a semi empirical method of analysis based on yield line theory. The coefficients give in code may be directly used to analyze the slabs.
However, the redistribution of moments is not permitted in this case.
Yield Line Theory
This is a limit state design or collapse load method developed by Johanson.
Also, read: Core Cutter Method
Difference Between One Way Slab and Two Way Slab
| Sr No. | One Way Slab | Two Way Slab |
| 1 | The one way slab is supported by a beam on two opposite side only. | The two way slab is supported by the beam on all four sides. |
| 2 | In one way slab, the load is carried in one direction perpendicular to the supporting beam. | In two way slab, the load is carried in both directions. |
| 3 | One way slab two opposite side support beam /wall | Two Way Slab four side mins all side supported beam /wall |
| 4 | One way slab is bend only in one spanning side direction while load transfer | Two way slab is bend both spanning side direction while load transfer |
| 5 | One way slab is bend only in one spanning side direction while load transfer | In two-way slab, the crank is provided in four directions. |
| 6 | If L/b the ratio is greater than or equal 2 or then it is considered a one-way slab. | If L/b the ratio is less than 2 then it is considered a two-way slab. |
| 7 | In one-way slab, the load is carried in one direction perpendicular to the supporting beam. | In two-way slab, the load is carried in both directions. |
| 8 | The deflected shape of the one-way slab is cylindrical. | Whereas the deflected shape of the two-way slab is a dish or saucer-like shape. |
| 9 | Chajja and Varandha are practical examples of one-way slab. | Whereas two-way slabs are used in constructive floors of the Multistorey building. |
| 10 | In one-way slab quantity of steel is less. | In two-way slab quantity of steel is more as compared to the one-way slab. |
| 11 | Main Reinforcement is in provide short span due to banding. | Main Reinforcement is in provide short span due to banding |
| 12 | Ly/Lx ≥ 2 one way slab spanning. | Ly/Lx < 2 two way slab spanning |
| 13 | One way slab near about 100mm to 150mm based on the deflection. | two way slabs is in the range of 100mm to 200mm depending upon |
| 14 | one way slab economical near about 3.5 m. | Two way slab may economical for the panel sizes near about 6m x 6m. |
What Is Slab?
A concrete slab is a common structural element of modern buildings, consisting of a flat, horizontal surface made of cast concrete. Steel-reinforced slabs, typically between 100 and 500 mm thick, are most often used to construct floors and ceilings, while thinner mud slabs may be used for exterior paving.
One Way Slab and Two Way Slab
The one–way slab is supported by a beam on two opposite side only. The two–way slab is supported by the beam on all four sides. In one–way slab, the load is carried in one direction perpendicular to the supporting beam. In two–way slab, the load is carried in both directions.
One Way Slab
One way slab is a slab which is supported by beams on the two opposite sides to carry the load along one direction. The ratio of longer span (l) to shorter span (b) is equal or greater than 2, considered as One way slab because this slab will bend in one direction i.e in the direction along its shorter span
One Way Slab Design
One–way slab is a type of concrete slab in which loads are transferred in one direction to the supporting beams and columns. Therefore, the bending occurs in only one direction. The design of one–way slab is simple and can be carried out easily. Slabs are used to provide flat, useful surfaces.
Two Way Slab Design
Two Way Slab Design by Direct Design Method as per ACI 318-11. The one-way slab is deflected in one way direction and primary reinforcement is placed in one direction whereas the two–way slab deflect in two directions and primary reinforcement placement is in two directions.
One Way Vs Two Way Slab
In one–way slab, the load is carried in one direction perpendicular to the supporting beam. In two–way slab, the load is carried in both directions. The deflected shape of the one–way slab is cylindrical. Whereas the deflected shape of the two–way slab is a dish or saucer-like shape.
Slab Reinforcement
In one way slab main reinforcement is parallel to shorter direction and the reinforcement parallel to longer direction is called distribution steel. In two way slab main reinforcement is provided along both direction. Slabs could be simply supported, continuous or cantilever.
What’s a Two Way?
wo–way means moving or working in two opposite directions or allowing something to move or work in two opposite directions. The bridge is now open to two–way traffic.
Difference Between One Way Slab and Two Way Slab
In one–way slab, the load is carried in one direction perpendicular to the supporting beam. In two–way slab, the load is carried in both directions. The deflected shape of the one–way slab is cylindrical. Whereas the deflected shape of the two–way slab is a dish or saucer-like shape.
Like this post? Share it with your friends!
Suggested Read –
- How to Structural Design a Building/House Step by Step Part-1 (One Way Simply Support Slab)
- How to Structural Design a Building/House Step by Step Part-2 (Two Way Simply Support Slab)
- How to Structural Design a Building/House Step by Step Part-3 (Slab Beam Design)
- How to Structural Design a Building/House Step by Step Part-4 (Column Design)
- Test for Compressive Strength of Brick | Water Absorption | Dimensions Test
- What Is Raft Foundation | Type of Footing | Detail of Raft Footin

Its like you read my mind! You seem to know so much about this, like you wrote the book in it or something.
I think that you could do with a few pics to drive the message home a bit, but instead
of that, this is excellent blog. A great read. I will
certainly be back.
very helpfull information sir
This web site is very educative.