What Is Bar Bending Schedule?
Important Point
Bar bending is calculating of steel quantity that calls bar bending schedule.
The preparation of bar bending schedules is one of the final stages in any concrete design following the preparation and detailing of the working drawings.
Whereas the procedure is generally straightforward, it does require a certain amount of calculation which can readily be carried out with the aid of a computer program.
The program in this section calculates the lengths of reinforcing bars required and outputs a bar bending schedule table together with the total weight of steel.
Also, read: What is Plum Concrete | Application | Mix Design | Methodology
Why Calculating of Bar Schedule?
- A requirement of steel in the project
- Labor cost
- Project monitoring
- Material reconciliation
- Contol of Wastage in steel etc..
As per the above point reason of bar bending schedule.
Also, read: Lab Test on Aggregates at Site
Preparation of Bar Bending Schedule as Per Bs 4466
As per BS (British Standard) 4466:1989
- Form of Schedule as Per Bs 4466
- Form of Fabric Schedule
- Preferred Shapes, Their Method of Calculation and Measurement of the Length
- Other Shapes, Their Method of Calculation and Measurement of the Length
- Minimum Former Radii, Book and Bend Allowances
- Scheduling
- Bends and Hooks
- Tolerances on Cutting and Bending Dimensions
Form of Schedule as Per BS 4466
From of Bar Schedule
-
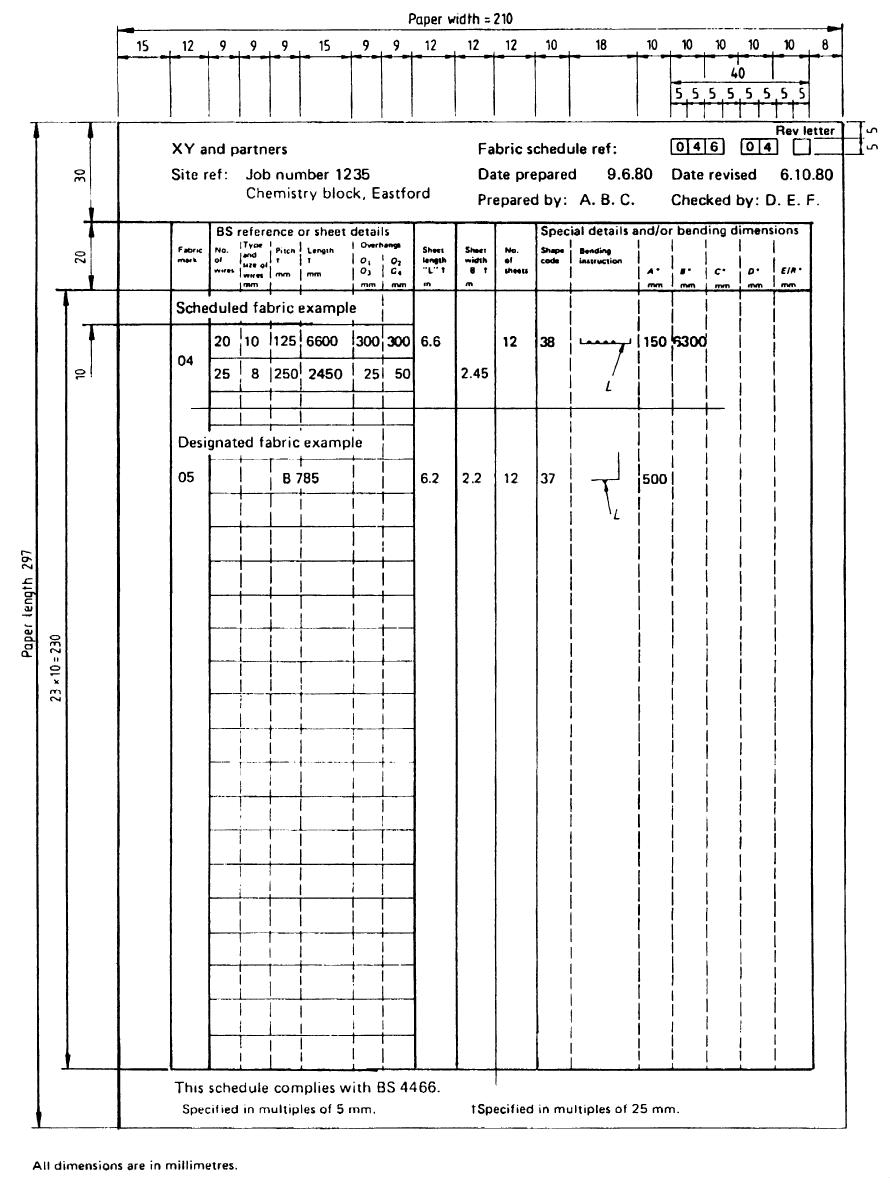
Form of Fabric Schedule as Per BS 4466
Form of fabric schedule
-
Preferred Shapes, Their Method of Calculation and Measurement of the Length
| Shape code | Method of measurement of bending dimensions | Total length of bar (L) measured along centreline |
|---|---|---|
| 20 | 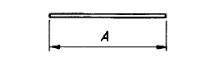 |
A |
| 32 | 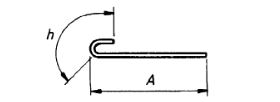 |
A + h |
| 33 | 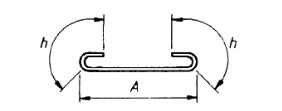 |
A + 2h |
| 34 | 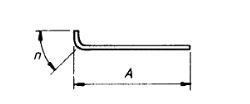 |
A + n Where the overall dimension of the bob is critical, use shape code 37 |
| 35 | 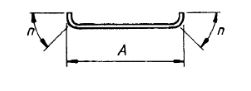 |
A + 2n Where the overall dimension of either bob is critical, do not use this shape code |
| 37 | 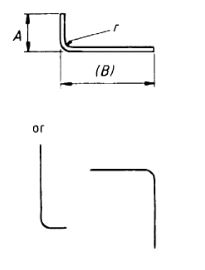 |
A + (B) –½r–d This formula is approximate Where r is greater than the minimum value inTable 3 use shape code 51 |
| 38 | 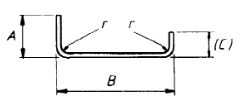 |
A + B + (C) –r –2d |
| 41 | 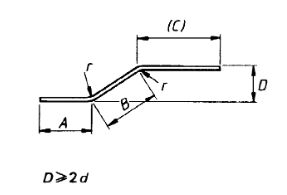 |
If angle with the horizontal are 45° or less,A + B + (C) length formula is near about and when bending angles exceed 45 ° the length could be calculated more accurately allowing for this difference between the specified overall the true length and dimensions measured along the central axis of this bar or wire. |
| 43 | 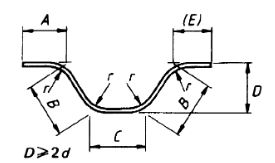 |
If angle with the horizontal are 45° or less,A + 2B + C + (E) length formula is near about and when bending angles exceed 45 ° the length could be calculated more accurately allowing for this difference between the specified overall the true length and dimensions measured along the central axis of this bar or wire. |
| 51 | 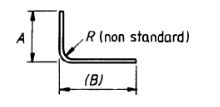 |
A + (B) –1/2R – d This formula is approximate R is minimum, use shape code 37If R is greater than 200 mm |
| 61 | 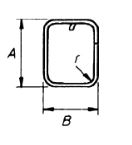 |
2(A + B)+ 12d Neither A nor B are to be less than 12d or 150 mm, whichever is the greater, for grade 460 in size not exceeding 20 mm nor less than 14d for size of 25 mm and over Neither A nor B are to be less than 10d for grade250 with a minimum value of A and B of 100 mm |
| 62 | 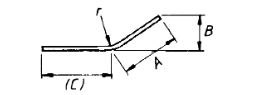 |
If angle with the horizontal is 45° or less,A + (C) |
| 82 | 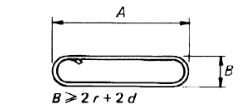 |
length formula is near about and when bending angles exceed 45 ° the length could be calculated more accurately allowing for this difference between the specified overall the true length and dimensions measured along the central axis of this bar or wire.2A + 3B + 18d If B is greater than 400 + 2 d |
Table: 1
Also, read: Total Station in Surveying | Operations | Advantage & Disadvantage | Types
-
Other Shapes, Their Method of Calculation and Measurement of the Length
| Shape code | Method of measurement of bending dimensions | Total length of bar (L) measured along centreline |
|---|---|---|
| 39 | 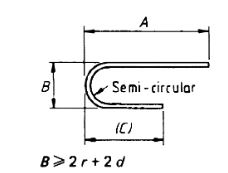 |
A + 0.57B + (C) –1.57dIf B is greater than400 + 2d, If B is greater than 400 + 2d |
| 42 | 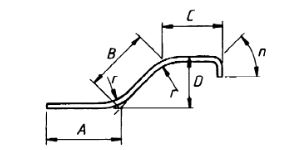 |
If the angle with horizontal is 45° or less, A + B + C + n |
| 45 | 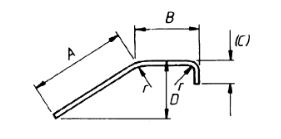 |
If the angle with horizontal is 45° or less A + B + (C) –1/2r –d |
| 49 | 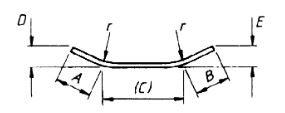 |
If the angle with horizontal is 45° or less, A + B + (C) |
| 52 | 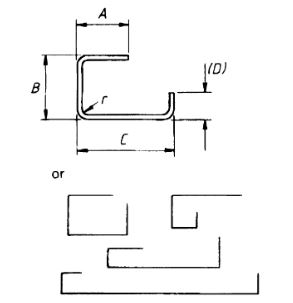 |
A + B + C + (D) –11/2r–3d |
| 53 | 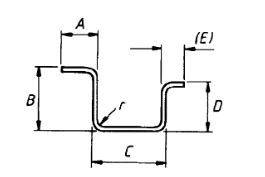 |
A + B + C + D + (E) –2r –4d |
| 54 | 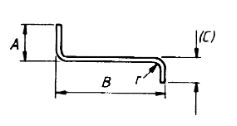 |
A + B + (C) – r + 2d |
| 55 | 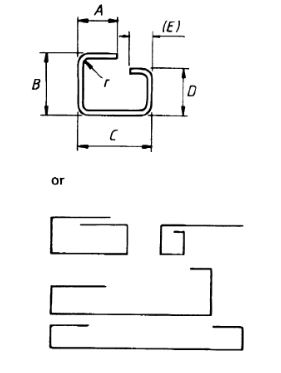 |
A + B + C + D + (E) – 2r – 4d |
| 65 | 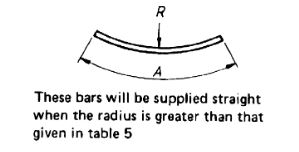 |
A |
| 77 | 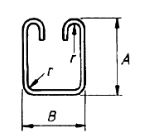 |
2A + B + 20d |
| 78 | 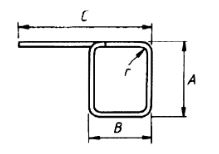 |
2A + B + C +3d |
| 79 | 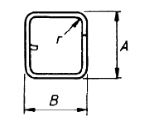 |
2A + 3B + 10d : Neither A nor B aren’t to be more than 12dor150mm, whichever is the greater, for grade460in sizes not exceeding 20 mm more than 14d for sizes of 25 mm and over. Neither A nor B aren’t to be more than 10d for grade250 with a minimum value of A and Bof100mm |
| 85 | 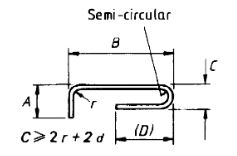 |
A + B + 0.57 C + (D) – 1/2r –2.57d IfCisgreaterthan 400 + 2d |
| 87 | 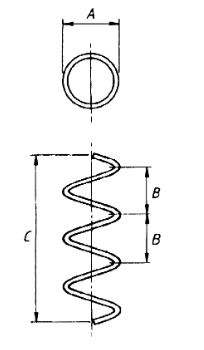 |
Where B is not greater than A/5 (C/B)π(A-d) (L≤12m) where A is the external dia (in mm)B is the pitch in helix (in mm)C is the overall height in helix (in mm)there B is greater than A/5 the formula doesn’t apply. There may be at least two full turns in the helix. |
Table: 2
Also, read: What Is Raft Foundation | Type of Footing | Detail of Raft Footing
-
Minimum Former Radii, Book and Bend Allowances
| Bar size | Grade and Type R and type and grade S | Grade and Type T and type and grade S | Fabric complying from BS 4483 | |||||||
| d | r | n | h | r | n | h | d | r | n | h |
| 6a | 12 | 100 | 100 | 18 | 100 | 100 | 5 | 15 | 100 | 100 |
| 8 | 16 | 100 | 100 | 24 | 100 | 100 | 6 | 18 | 100 | 100 |
| 10 | 20 | 100 | 100 | 30 | 100 | 110 | 7 | 21 | 100 | 100 |
| 12 | 24 | 100 | 110 | 36 | 100 | 140 | 8 | 24 | 100 | 100 |
| 16 | 32 | 100 | 150 | 48 | 100 | 180 | 9 | 27 | 120 | 135 |
| 20 | 40 | 100 | 180 | 60 | 110 | 220 | 10 | 30 | 120 | 135 |
| 25 | 50 | 130 | 230 | 100 | 180 | 350 | 12 | 36 | 130 | 145 |
| 32 | 64 | 160 | 290 | 128 | 230 | 450 | — | — | — | — |
| 40 | 80 | 200 | 360 | 160 | 280 | 560 | — | — | — | — |
| 50a | 100 | 250 | 450 | 200 | 350 | 700 | — | — | — | — |
Table: 3
Also, read: What is Chain Surveying (Principal, Procedure, Method, Instrument)
Scheduling
-
Each sheet or bar of fabric should be scheduled completely and without any reference to earlier schedules. Such as descriptions “See schedule 12” or “As before” shall not be used
- The preferred shape codes to be used shall be as given in Table 1. Table 2 gives other shape codes that may be required. Shapes that do not have a specific shape code number given in Table 1 or Table 2
- For shapes without an end anchorage, the
dimension shown in parentheses in Table 1 and Table 2 shall be the variable dimension to allow for the permissible deviations - No dimension given in Table 1 or Table 2 shall be given a zero value, as this changes the basic shape.
- If the angle between both portions of the shaped meeting at a bend isn’t a right angle, it should be given and shall be defined by co-ordinates and not by degrees of arc.
- The overall off-set dimension of a crank should be not less than twice the size of the bar or wire.
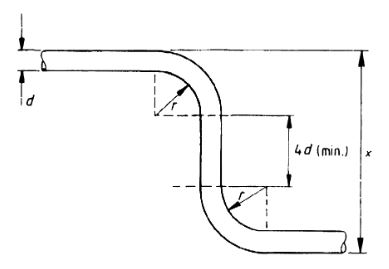
- The angled length as shown in Figure 6 shall be not less than 10d for grade 250 nor less than 12d for grade 460 in sizes of less than 20 mm nor less than 14d for grade 460 in sizes of 25 mm and over.
-
Or all shapes with two or more bends into the same or opposite directions, the overall dimension is given on the schedule shall always include a minimum straight of 4d between the curved portion of the bends, as shown in as per the below figure. The value of x in as per below figure shall be not less than the following:
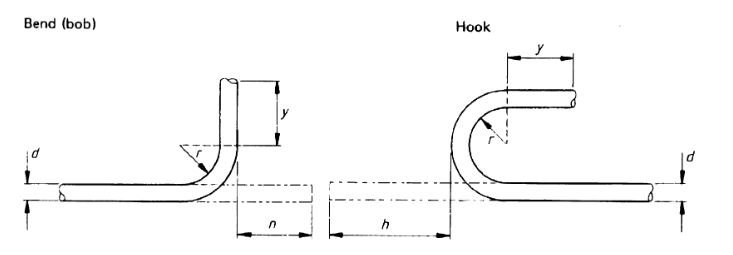
- The minimum length of material to be given on this schedule to form a hook or bend shall be as given for n or h respectively inTable 3.
Also, read: What Is Bulkage of Sand (Fine Aggregate )
Bends and Hooks
- Before taking into account the cumulative cutting tolerances, the nominal value for y in table 3 shall be calculated as follows:
-
-
For a bend, n – 0.57r+ 0.21d;
-
For a hook, h–2.14r– 0.57d
-
Tolerances on Cutting and Bending Dimensions
- The tolerances given in Table 4 shall apply for cutting and/or bending dimensions and should be taken in the account then completing the schedule. The end anchorage or the dimension in parentheses into the shape codes given inTable 1 and Table 2 shall be used to allow for any permissible deviations resulting from cutting and bending.
| Description | Tolerance in mm |
| Cutting of straight lengths (including reinforcement for | + 25 |
| Subsequent bending) | — 25 |
| Bending < 1 000 | +5 up to -5 |
| > 1 000 mm to < 2 000 mm | +5 up to -10 |
| > 2 000 mm | +5 up to -25 |
Cutting and bending tolerances
Also, read: Soundness of Cement Test
Radius of Bending in Reinforcement
- Reinforcement to be formed into a radius exceeding that given in Table 5 shall be supplied straight.
| Bar size (mm) | — | 6 | — | 8 | — | 10 | 12 | 16 | 20 | 25 | 32 | 40 |
| Wire size (mm) | 5 | 6 | 7 | 8 | 9 | 10 | 12 | — | — | — | — | — |
| Radius (m) | 2.4 | 2.5 | 2.6 | 2.8 | 3.0 | 3.5 | 4.3 | 7.5 | 14.0 | 30.0 | 43.0 | 58.0 |
Like this post? Share it with your friends!
Suggested Read –
- Para Pit
- What is Consistency of Cement
- What Is Cement | Type of Cement
- What Is Soundness of Cement Test
- What Is Water Cement Ratio | Water-Cement Ratio and Concrete Strength | Role of Water in Concrete
- What Is Unit Weight | What Is Density | What Is Unit Weight Material | Unit Weight Building Materials


Leave a Reply