Design Considerations:
Important Point
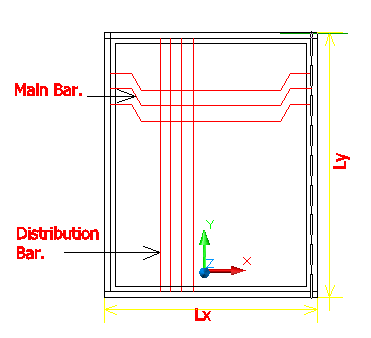
One Way Slab
1. Effective Depth (d)
For deflection control
L/d = 20 X M.F
- M.F. Modifiction factor from— IS: 456, p.38.Fig-4
- Assume % steel 0.3 to 0.6%
Fs = 0.58 Fy X (Ast requierd / Ast Provied)
Initially assume that Ast reqierd = Ast Provided
Fy = 250 N/ Sq.mm —– Fs = 0.58 X 250 = 145 N/ sq.mm.
Fy = 415 N/ Sq.mm —– Fs = 0.58 X 415 = 240 N/ sq.mm.
Fy = 500 N/ Sq.mm —– Fs = 0.58 X 500 = 290 N/ sq.mm.
2. Effective Span:
ClearSpan + d
c/c of Supports
Whichever is smaller ——– as per IS 456-2000 P. 34, CI 22.2.a
3. Reinforcement Requirements
Minimum reinforcement
For Fe-250 Pt = 0.15 % of total C/s area (d x D)
For Fe-415 Pt = 0.12 % of total C/s area (d x D)
For Fe-500 Pt = 0.12 % of total C/s area (d x D) ——– as per IS 456-2000 P. 48, CI 26.5.2.1
Maximum diameter (Sp 34)
For minbar:
- Plain bars———–10 mm Ø min dia
Deformed bars—–8 mm Ø min dia
For Distribution bars:
- Plain bars———–6 mm Ø min dia
Deformed bars—–6 mm Ø min dia
4. Check for Cracking
For Min Steel:
3d ——— Where. d = Effective depth
300mm
Spacing should not exceed smaller these two values.
For Distribution steel:
5 d
450mm
Spacing should not exceed smaller these two values. ——- IS: 456-2000, P.46
5. Check for Deflection:
Allowable L/d = 20 X M.F.
- M.F is Obtained from IS:456-200 P-38 Fig 4
Find actual, L/d
If Actual L/d < allowable L/d ———- Ok
6. Check for Development Length (Ld)
IS 456-2000,P.44, Cl. 26.2.3.3 C
Ld should be ≤ 1.3 (M1/V) + L0
Where
Ld = (Ø.σs / 4 τ bd )—————–σs = 0.87 fy As per IS 456-200, P.42
50 % of steel is bent up near support. Therefore find M.R for 50 % of steel only
M1 = M.R. for 50% steel support
V = Shear force at the support
L0 = Sum of anchorage beyond the centre of support
d
12 Ø
Take L0 as the smaller of two values.
Also, read: What is Chain Surveying (Principal, Procedure, Method, Instrument)
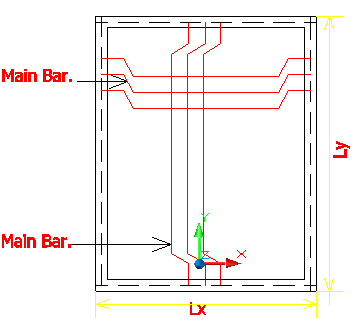
Two Way Slab
1. Effective Depth (d):
- For deflection control
- L/d = 35 X M.F X 0.8
- M.F. Modifiction factor from— IS: 456, p.38.Fig-4
- Assume % steel 0.3 to 0.6%
- Fs = 0.58 Fy X (Ast requierd / Ast Provied)
- Initially assume that Ast reqierd = Ast Provided
- Fy = 250 N/ Sq.mm —– Fs = 0.58 X 250 = 145 N/ sq.mm.
- Fy = 415 N/ Sq.mm —– Fs = 0.58 X 415 = 240 N/ sq.mm.
- Fy = 500 N/ Sq.mm —– Fs = 0.58 X 500 = 290 N/ sq.mm.
2. Effective Span:
- ClearSpan + d
- c/c of Supports
Whichever is smaller ——– as per IS 456-2000 P. 34, CI 22.2.a
3. Load Calculations:
- Total Load = D.L. + F.L. + L.L.
- Dead load of slab = (d x 25)
- Floor Finishing load = (as floor finishing near 1 kn/sq.mm)
- Live load = ( as per calculation)
- Factor Load = 1.5 x Total load
4. Mid Span Moment:
Corners not held down conditions is given as per IS: 456-2000 P-90 CI D-2
Mx = ax . w . lx. lx
My = ay. w . lx. lx
ax and ay coefficient are obtained from IS 456 tables -26, fig 10.3 shoe nine separate possible arrangement for a two-way restrained slab.
5. Effective Depth of Flexure:
Mu = 0.138 . fck . b.d.d
Heaer find d
Mu = Sp 16 P 10 Table C
Fck = strength of concrete
b = 1 m area required load
6. Reinforcement in Mild Strip :
Along Lx
- Pt= 50 (fck/fy)x( 1-√(1-(4.6xMu/Fck b.d.d)))
- fck = strenth of concrete
- fy = 415 N/Sq.mm
- Mu = Sp 16 P 10 Table C =0.138 . fck . b.d.d= Mx
Along Lx
- Pt= 50 (fck/fy)x( 1-√(1-(4.6xMu/Fck b.d.d)))
- fck = strenth of concrete
- fy = 415 N/Sq.mm
- Mu = Sp 16 P 10 Table C =0.138 . fck . b.d.d= My
7. Check for Cracking:
Along with Lx:
3d ——— Where. d = Effective depth
300mm
Spacing should not exceed smaller these two values.
Along with Ly:
3d ——— Where. d = Effective depth
300mm
Spacing should not exceed smaller these two values.
8. Check for Deflection:
Allowable L/d = 35 X M.F.X 0.8
- M.F is Obtained from IS:456-200 P-38 Fig 4
Find actual, L/d
If Actual L/d < allowable L/d ———- Ok
9. Check for Development Length:
IS 456-2000,P.44, Cl. 26.2.3.3 C
Ld should be ≤ 1.3 (M1/V) + L0
Where
Ld = (Ø.σs / 4 τ bd )—————–σs = 0.87 fy As per IS 456-200, P.42
50 % of steel is bent up near support. Therefore find M.R for 50 % of steel only
M1 = M.R. for 50% steel support
V = Shear force at the support
L0 = Sum of anchorage beyond the centre of support
d
12 Ø
Take L0 as the smaller of two values.
Like this post? Share it with your friends!
Suggested Read –
- Road Development Plans in India
- What Is Scaffolding | Types of Scaffolding
- What Is Dry Pack Mortar | Advantages of Dry Pack Mortar | Disadvantages of Dry Pack Mortar
- Difference Between Whole Circle Bearing and Quadrantal Bearing | What Is WCB | What Is QB
- What Is Injection Grouting | Types of Injection Grouting | Different Types of Grouting Materials
- What Is Hempcrete | Hempcrete Blocks | Advantages & Disadvantages of Hempcrete Blocks | Applications of Hempcrete
- What Is Hard Hat | Hard Hat Colour Definition | Different Hard Hat Colour Codes | Types of Safety Helmets | Classification of Hard Hats


Leave a Reply