What Is Modulus of Rupture | What Is Flexural Modulus | What Is Flexural Stress | Flexural Strength of Concrete | Bending Modulus | What Is Flexural Strength

Modulus of Rupture of Concrete Beam:

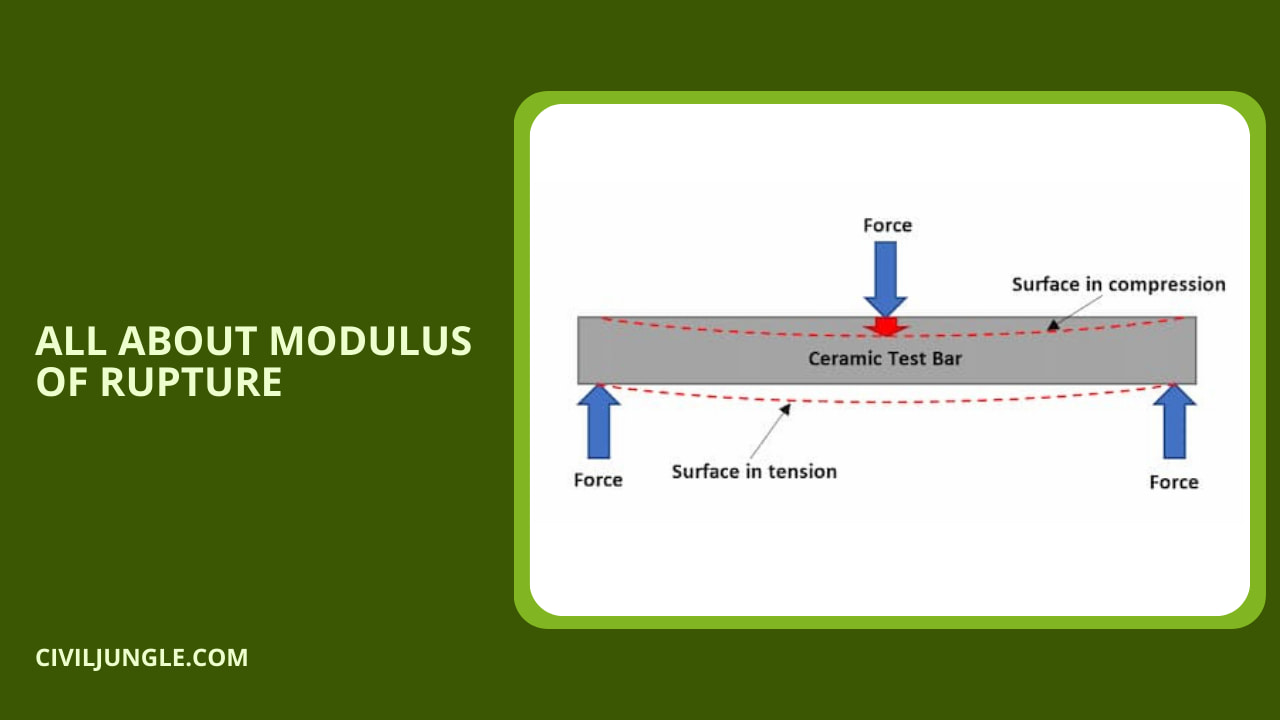
Modulus of rupture of Concrete beam indicates the amount of compression and force the unstable beam can withstand under any condition and its resistance to bending.

What Is Modulus of Rupture?

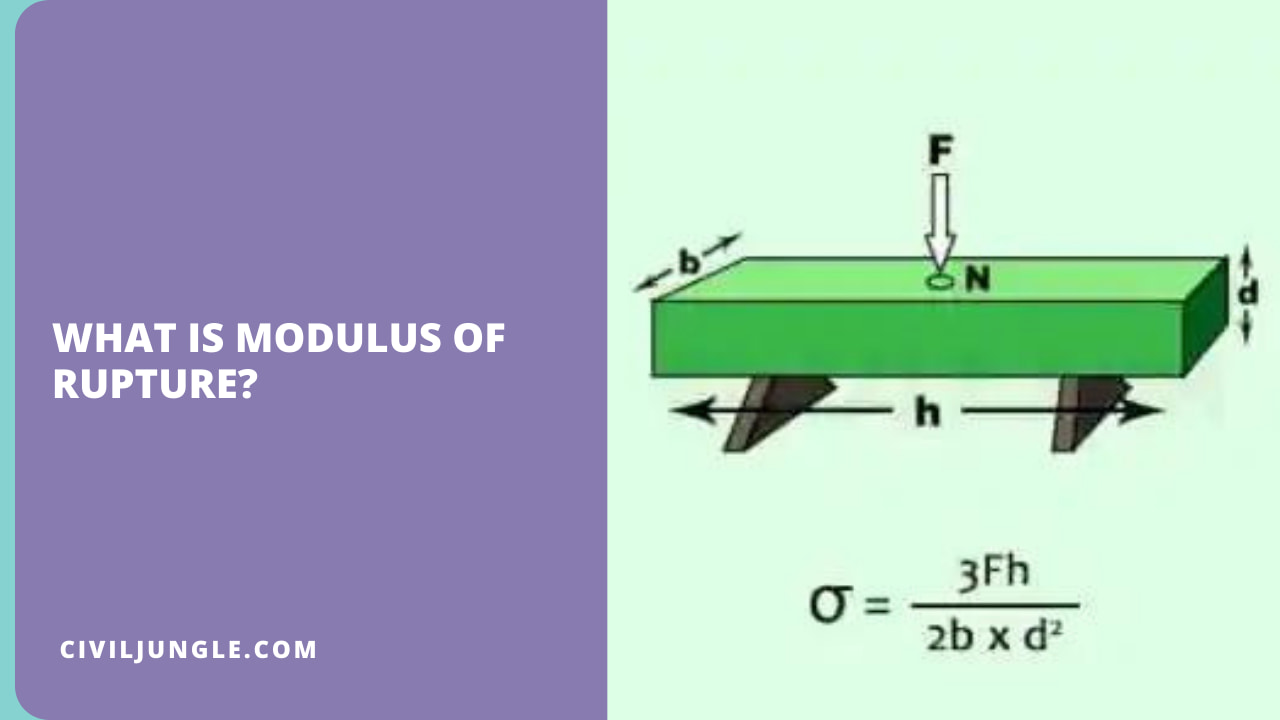
Modulus of rupture measures the strength of civil construction parts like concrete, beams, or slabs. Modulus of rupture is also known as flexural strength, bend strength, or fracture strength.

The modulus of rupture determined by the loading of the third point is less than the modulus of rupture determined by the loading of the center point, sometimes up to 15%.

Modulus of Rupture is defined as the final strength related to the failure of the beams by the flexibility equal to the moment of bending in the fracture divided by part of the beam section.

The calculation of the modulus of rupture is considered important for construction equipment for the following reasons. The calculation from Modulus of Rupture helps us to build structural elements such as beams, cantilevers, shafts, etc.

It provides a parameter for the development of dynamic building materials. It is a predictive tool for both resistance and durability of the construction project.

---

• Rate Analysis of Concrete
• All About Concrete Expansion Joint | Types of Concrete Expansion Joints
• Difference Between Flexible Pavement and Rigid Pavement | What is Pavement | Types of Pavement
• All About Mastic Asphalt Flooring | What Is the Meaning of Mastic Floor | Mastic Asphalt Flooring Cost | Where Is Asphalt Flooring Used
• What Is Folded Plate | Folded Plate Structure | Folded Plate Roof Construction Details | Folded Plate Staircase | What Are Folded Plate Roofs
• What Is a Cavity Wall | How to Build a Cavity Wall | Cavity Wall Detail | Cavity Wall Thickness | Cavity Wall Insulation Pros and Cons | Brick Cavity Wall

---

What Is Flexural Modulus?

• In mechanics, the flexural modulus or bending modulus is a powerful material that is calculated as a measure of stress pressure on the flexural flexion or inclination of an object that resists bending.
• Flexural Modulus is determined from the slope of the pressure curve formed by the flexural test (such as ASTM D790) and uses power units in each position.
• The flexural modulus described using a three-point curve test takes the stress line response.
• Ideally, the flexibility or bending of the stiffness mode is similar to the tensile modulus (Young’s modulus) or the compression modulus of elasticity. In fact, these values ​​may vary, especially in polymers which are usually viscoelastic (time-dependent) materials.
• The alignment of the flexural modulus with Young’s modulus also takes the corresponding model of pressure and stiffness as the bend models have strong and compressive pressures. Polymers in particular, have different types of compression and stiffness of the same material.
• Flexural modulus of rupture is about 10% to 20% of the compressive strength, depending on the type, size, and volume of the awesome aggregate used in the concrete block.

What Is Flexural Stress?

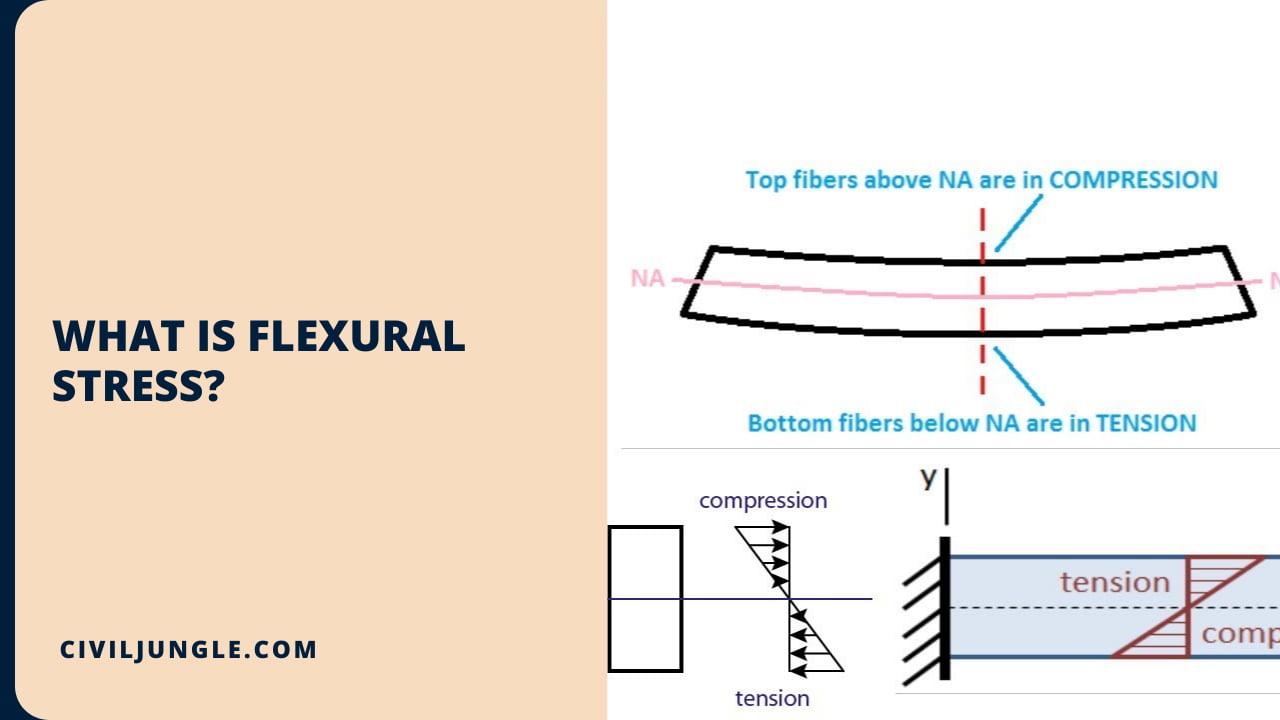
The stress caused by the bending moment in a structural member is known as Flexural Stress or Bending Stress. Flexural Stress or Bending Stress usually occurs in two cases.

One case is called bending of simply support beams and the other case is called bending of cantilever beams. Flexural Stress for simply supported structural beams acts on the two surfaces differently.

The upper surface of the bending beam is in compression stress and the bottom surface of the beam is in tension stress. The neutral axis or the center axis of the beam is a region of zero stress.

The flexural stress (σ) is defined by the formula σ = MC / I. In the above formula, M = Bending moment, which is calculated by multiplying the force by the distance between that point of interest and force. C = Distance from Neutral Axis and I = moment of inertia.

Flexural Stress of cantilevered beam also has a similar formula. The M, C, and I formulas can be complex, depending on the exact configuration and structure of the beam.

---

• Top 10 Construction Companies in India
• House Construction Cost Calculator Excel Sheet
• How to Building Construction Process Step by Step
• Types of Construction Project | What Are Construction Projects | How Many Types of Construction Are There
• Top-Down Construction | What Is a Top-Down Construction | Advantages & Disadvantages of Top-Down Construction
• 20 Vastu Tips Before House Construction | Vastu Tips for Different Locations of House | Scientific Facts of Vastu Location of Rooms
• What Is Road Pattern | Different Types of Road Patterns | Grid Pattern Definition | Radial Pattern | Rectangular or Block Pattern | Minimum Travel Pattern

---

Flexural Strength of Concrete:

1. Flexural Strength of Concrete is the ability of a beam or a slab of concrete to withstand failure.
2. Flexural strength of concrete is a measure of the strength of concrete strength and resistance to failure is a measure of unstable concrete slab or slab.
3. The relative flexural strength and contrast or requirements should be based on the same aggregate size and loading adjustment. Modulus of Rupture measured on a third-point load (ASTM C78) is lower than that determined by the average point load (ASTM C293), sometimes 15 percent
4. Flexural strength of concrete is approximately 10 to 15 percent of the compressive force depending on the size of the compound and the type, size and volume of the compound used.
5. For structural members of a concrete structure, the Modulus of Rupture rating is obtained by the equation F_r = 7.5 (f_c’)
6. Here, F_r is the Modulus of Rupture.
7. F_c’ is the specified compressive strength.
8. Here Modulus of Rupture is critical in the construction design; the best measurement is established from laboratory tests of specific compounds and materials used.
9. Flexural strength is one measure of the strength of concrete strength. It is the standard of a fixed beam or slab to withstand bending.

---

• Difference Between One Way Slab and Two Way Slab | What is Slab
• Emulsion Paint Vs Oil Based Paint | Purpose of Providing Paints | Properties of Good Paint | Properties of Good Paint | What Is Oil Based Paint
• Is Steel Stronger Than Concrete | Steel and Concrete Construction Costs | Steel Vs Concrete | How Strong Is Concrete | Concrete Vs Steel Building Cost
• Skeleton Frame | What Is Building Skeleton | What Is Steel Structure Building | Use of Steel Frame Structures| Advantages & Disadvantage of Steel Frame
• Components of Space Frame System | Types of Space Frame | Advantages & Disadvantages of Space Frame Structure | Space Frame Structures Examples
• What Are Plastic Roads | How to Make Plastic Roads | Who Invented Plastic Roads | First Man Made Plastic Road | Advantages & Disadvantages of Plastic Roads

---

Bending Modulus:

Rigidity (or stiffness) is the property of a polymer defined by the Flexural modulus or bending modulus of stiffness. Bending Modulus is therefore one of the most important of properties of solids material.

Bending Modulus refers to the ability of an object or material to bends. It is a measure of rigidity or resistance to bending when force is applied differently at the long edges of a sample also known as a three-point bending test.

The Bending modulus is represented by the slope of the first part of the straight line of the stress curve and is calculated by dividing the change in stress by a change corresponding to the strain.

Therefore, Bending Modulus is also known as the ratio of measurement of stress to strain.

What Is Flexural Strength?

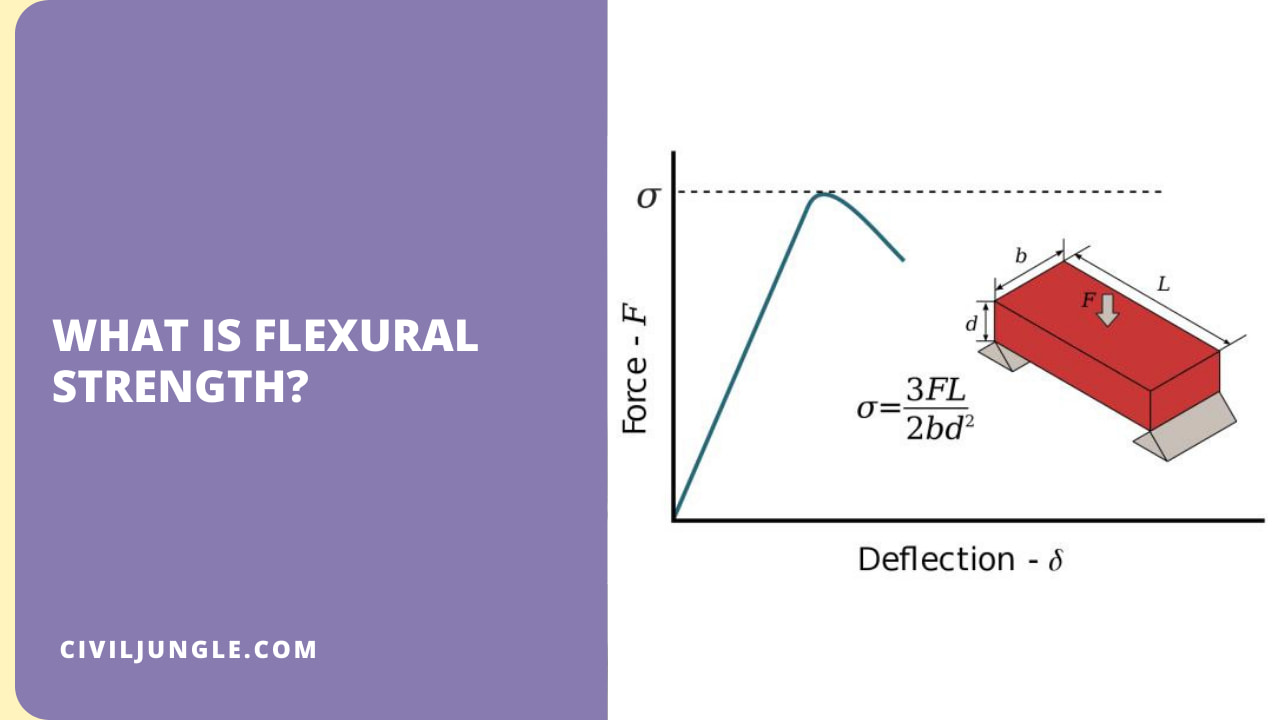
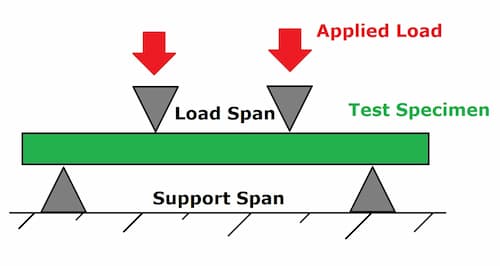
Flexural strength is an indirect measure of the strength of concrete strength. It is a measure of the high pressure on the surface of the thickness of the reinforced concrete beam or slab where it fails to bend. It is measured by loading 150 x 150-mm (or (100 x 100-mm) concrete beams with a span length of at least three times.

Flexural strength is about twelve to twenty percent of compressive strength, depending on the type, size, and volume of coarse aggregate used.

Flexural strength is expressed as the “Modulus of Rupture” (MR) in MPa and is determined by standard test methods ASTM C78 (third point loading) or ASTM C293 (intermediate loading). Flexural strength helps us to judge the quality of the materials used in construction.

Flexural Strength Formula:

Flexural strength of a beam can be calculated using the equation

F = (PL)/ (2bd).

Here,

• F = Flexural strength of concrete (in MPa).
• P = Failure Load (in N)
• L = Effective span of the beam (in mm).
• b = Breadth of the beam (in mm).
• d = Depth of the beam (in mm).

Modulus of Rupture Formula:

The breakdown Modulus of Rupture Formula varies with a different types of system loading.

#1. For first system, a rectangular sample under a load on a three-point bend setup.

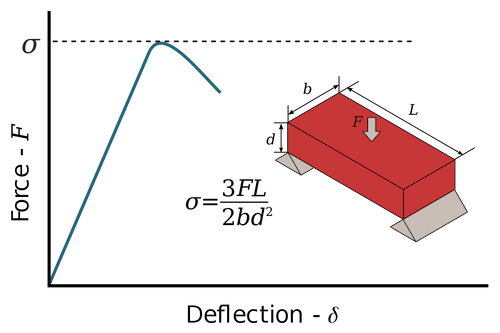
Modulus of Rupture = (3FL)/(2bd²)

Here,

• F = load (force) at the cracked point (N).
• L = Total length of the support span.
• b = Total width of the support span.
• d = Total thickness of the support span.

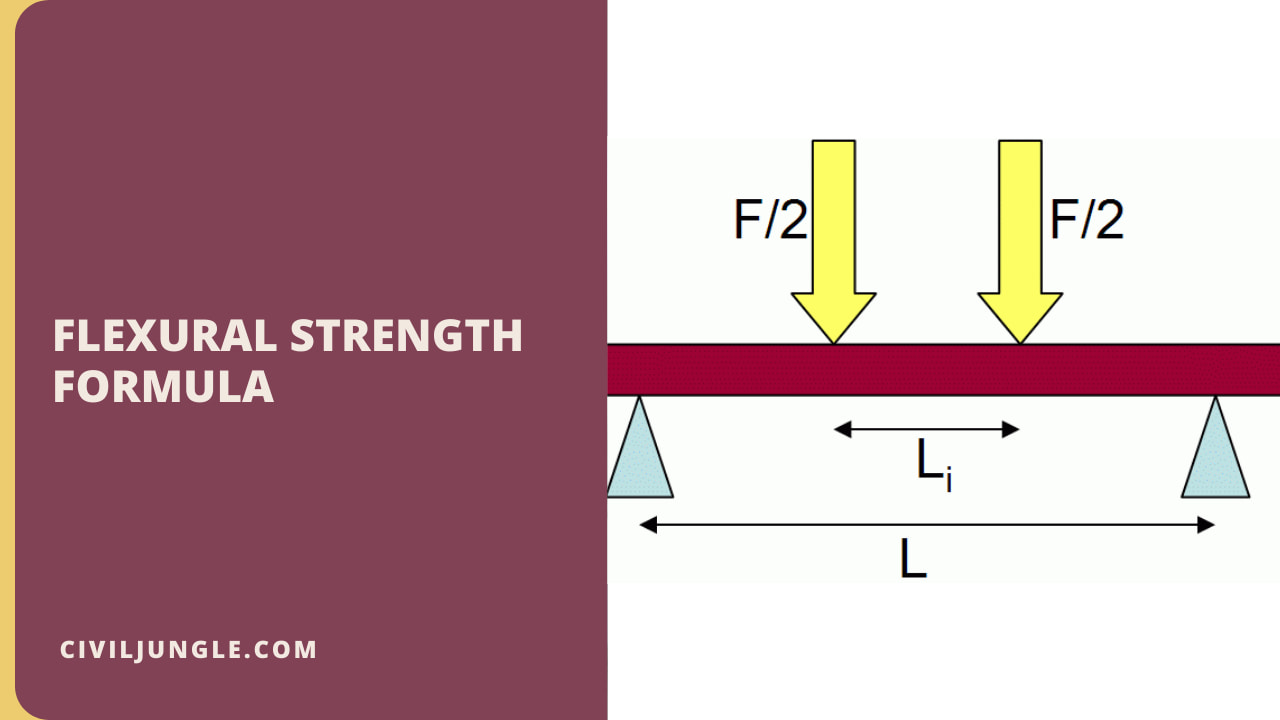
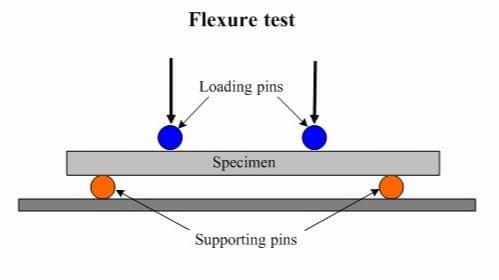
#2. For the second system, a rectangle sample under a load on a four-point bend setup, where the loading span is one third the length of the support span.

Modulus of Rupture = (FL)/(bd²)

Here,

• F = load (force) at the cracked point (N).
• L = Total length of the support (outer) span.
• b = Total width of the support (outer) span.
• d = Total thickness of the support (outer) span.

#3. For the third system, a rectangle sample under a load on a four point bend setup, where the loading span is half the length of the support span.

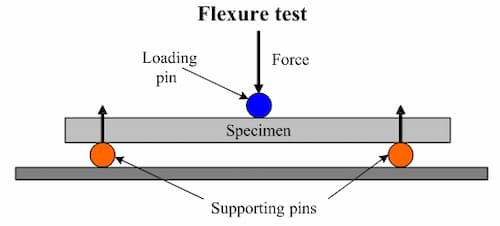
Modulus of Rupture = (3FL)/(4bd²)

Here,

• F = load (force) at the cracked point (N)
• L = Total length of the support span.
• b = Total width of the support span.
• d = Total thickness of the support span.

#4. For the last system, a rectangle sample under a load on a four point bend setup, where the loading span is neither one third nor half the support span.

Modulus of Rupture = (3F[L-L_i])/(2bd²)

Here,

• F = load (force) at the cracked point (N).
• L = Total length of the support (outer) span.
• L_i = Total length of the loading (inner) span.
• b = Total width of the support (outer) span.
• d = Total thickness of the support (outer) span.

---